| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Deeplearning
- 주가예측
- 빅데이터
- pandas
- 머신러닝
- 데이터분석
- AI
- Hadoop
- R시각화
- ggplot
- 데이터처리
- lstm
- 빅데이터처리
- 딥러닝
- NLP
- 데이터시각화
- SQL
- word2vec
- 기계학습
- 그래프시각화
- R프로그래밍
- R그래프
- 자연어처리
- 데이터
- HIVE
- 하둡
- r
- Python
- CNN
- 그래프
- Today
- Total
욱이의 냉철한 공부
[통계기초] 확률변수와 확률분포함수 : 이산확률 본문
* 자료출저 및 참고강의
패스트캠퍼스 올인원 패키지(금융공학/퀀트) 장순용 강사님 인터넷 강의
명지대 산업경영공학과 박윤선 교수님 통계학개론 강의
* 목차
1. 확률변수
2. 확률분포함수(probability distribution function)
3. 모집단과 모수
4. 이산확률
5. 이산확률 : 베르누이 확률분포(Bernoulli)
6. 이산확률 : 이항확률분포(Binomial)
7. 이산확률 : 푸아송확률분포 (Possion)
1. 확률변수(random variable)
- 확률변수(random variable)
실험의 결과에 수치를 대응시키는 변수를 확률변수라 하고 영문 대문자 X, Y, Z..로 나타낸다.
즉 확률변수는 표본공간(S)의 모든 단순사건에 수치를 대응시키는 함수
표본공간(S)상의 확률을 실수 확률로 대응
종류 : 이산확률변수(discrete random variable), 연속확률변수(continuous radom variable)
ex) 동전을 한번 던지는 실험에서 앞면(H)이 나오면 1, 뒷면(T)이 나오면 0
- 이산확률변수(discrete random variable)
셀 수 있는 가지수의 값을 가지는 확률변수
ex) 주사위를 던져서 나오는 눈의 수 : {1,2,3,4,5,6}
- 연속확률변수(continuous random variable)
셀 수 없는(무한대) 가지수의 값을 가지는 확률변수
ex) 1년 연봉, 성인남성의 신장
2. 확률분포함수(probability distribution function)
- 확률분포(probability distribution)
확률분포(probability distribution)는 미래에 발생할 사건에 대해 확률을 나열한 것
확률변수의 값 또는 구간에 대해서 확률을 대응 시켜주는 관계
여러가지 대안 가운데 하나를 선택해야 하는 경우 정보 양이 많을수록 유리.
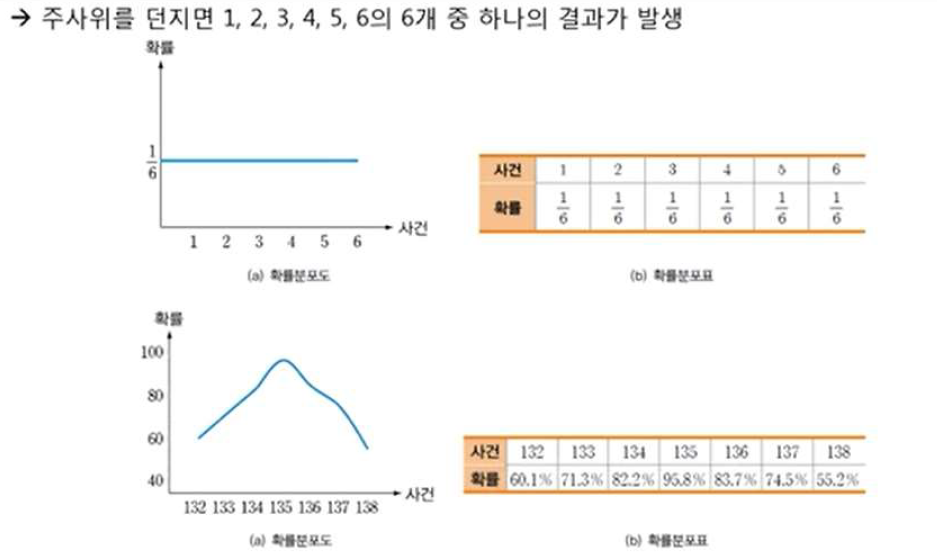
- 이산확률분포함수
이산확률변수가 가지는 값과 이것의 확률 사이의 대응관계.
확률변수는 영문 대문자, 확률변수의 값은 영문 소문자로 표기
확률변수 X의 값이 x일 확률은 P(X=x) 또는 P(x)로 표기
ex) 확률변수 X, 확률변수의 값 x

- 이산확률의 필수조건
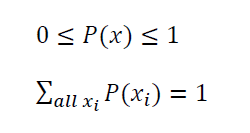
- 연속확률분포함수(확률밀도함수)
이것을 사용하여 연속확률변수의 값이 특정 구간에 속할 확률을 나타냄.
3. 모집단과 모수
- 모집단(population)
분석 대상 전체를 의미, 실존 또는 개념적 존재
통계분석을 적용할 관심 대상의 전체집합
- 모수(parameter)
모집단의 특성을 나타냄
모집단을 분석하여 얻어지는 결과수치
ex) 모평균, 모분산, 모표준편차
모집단의 특성을 묘사하기 위해서 확률분포함수를 사용함.
ex) 모평균을 확률분포함수를 사용하여 계산
* 확률분포를 확인하고 알 수 있는 것 3가지 (확률분포를 이용하여 모집단을 기술 가능)
1) 분포모양
2) 통계값 : 평균, 분산
3) 이상치
4. 이산확률
- 이산확률을 따르는 모집단의 평균(모평균)
모평균은 확률변수 X의 기대값(expected value)이라고도 불리우며 E[X]로 나타냄.
이산확률변수가 가질 수 있는 값들에 확률을 가중치로 곱해서 평균을 구한것.

- 모평균의 법칙

- 이산확률을 따르는 모집단의 분산 (모분산)
확률변수 X의 모분산을 Var(X)와 같이 나타내기도 함.
모평균을 기준으로한 편차의 제곱에 확률을 가중치로 곱해서 평균을 구한것


- 모분산의 법칙

- 예시 문제

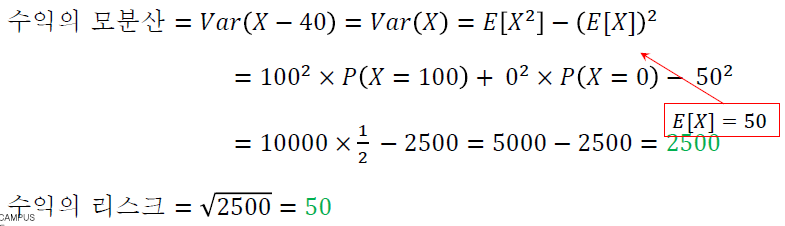
5. 베르누이 확률분포(Bernoulli)
- 베르누이 확률분포 개요
-> 한 번 시행

베르누이 시행을 확률분포로 나타낸 것을 베르누이확률분포라고 명칭함.
베르누이 시행은 서로 반대되는 사건이 일어난 실험을 반복적으로 실행하는 것을 명칭함
베르누이 시행에는 두 개의 가능한 값이 있음
그런데 성광확률을 p(x=1인 경우)라 할 때, 실패확률은 1-p(x=0인 경우)라고 가정.
=> 베르누이 시행에서 P(X=1) = p이고, P(X=0) = (1-p)
ex) 1 또는 0, 동전의 앞면(H) 또는 뒷면(T), "성공" 또는 "실패"

- 베르누이확률분포 함수
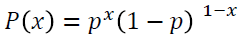
- 표현
확률변수 X가 베르누이 확률분포를 따른다 : X~Ber(p)
- 통계값
평균 : p, 분산 : p(1-p), 표준편차 : √p(1-p)

6. 이항확률분포(Binomial)
- 이항확률분포 개요
-> 여러번 시행

이항확률분포는 연속적인 베르누이 시행을 거쳐 나타내는 확률분포임.
이항확률변수 Xbin은 0또는 1의 값을 갖는 n개의 독립적인 베르누이확률변수 Xber를 더한 것
Xbin = Xber + Xber + .... Xber
쉽게 말하여 두 개의 서로 다른 사건이 배타적으로 계속 발생하는 경우
ex) 동전 하나를 n번 던져서 앞면(H)이 나온 횟수를 집계.
n회 시행하여 "성공"한 횟수를 더한다.
- 이항확률분포 함수

소문자 p는 개개 베르누이확률변수의 값이 1과 같을 확률.
x는 0과 n사이의 숫자
- 표현
확률변수 X가 이항 확률분포를 따른다 : X~Bin(n,p)
- 통계값
평균 : E[Xbin] = E[Xber] + E[Xber] .... E[Xber] = nE[Xber] = np
분산 : Var(Xbin) = Var(Xber) + ..... + Var(Xber) = nVar(Xber) = np(1-p)
=> 서로 독립적이다.
표준편차 : √np(1-p)
- 이항확률분포



- 이항확률변수의 합
서로 독립적인 확률변수 X와 Y가 다음과 같이 이항 확률분포 따를 때, X~Bin(n,p), Y~Bin(m,p)
: X+Y ~ Bin(n+m, p)
why? : X+Y ={Xber+Xber+....+Xber} + {Xber+...+Xber}
- 예시 문제

7. 푸아송확률분포 (Possion)
- 푸아송확률분포 개요
유래 : 푸아송확률분포는 프랑스의 과학자 Simeon Poisson의 이름에서 유래
일정 시간 또는 공간에서 발생하는 사건(성공)의 횟수(count)에 대한 이산확률분포이다.
특정한 사건이 발생할 가능성이 매우 드문 경우의 확률분포임.
- 예시
시간당 수신하는 이메일의 개수
특정 지역(국가)의 년간 지진의 발생 횟수.
초콜렛 칩 쿠키에 박힌 초콜렛 조각의 개수
=> 포아송분포하고 지수분포하고 같다.
일상생활에서 이루어지는 분포는 포아송 분포와 지수분포
- 푸아송확률분포 표현
확률변수 X가 푸아송 확률분포를 따른다.

- 푸아송확률분포 함수

λ는 유일한 파라미터이고 양의 수치여야 함.
한 단위 시간 또는 공간에서 발생하는 사건(성공)횟수의 평균.
발생률 또는 성공률이라고 해석.
x는 0이상의 숫자 이어야 함 : 0<=x
- 통계값
푸아송 확률변수의 평균과 분산은 동일

- 푸아송확률분포
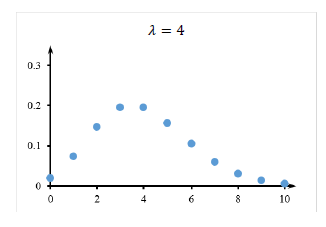

- 푸아송확률분포와 이항확률분포의 관계
둘 다 이산확률
이항확률변수의 평균 : np
푸아송확률변수의 평균 : λ
이항확률변수의 평균에서 n을 키움과 동시에 p를 줄이면, 이항확률은 푸아송확률에 수렴
즉 p = λ/n과 같이 선택
ex) X~Bin(10000,3/10000) => X~Poisson(m=3)

* 두 분포(이항확률분포, 푸아송확률분포) 모두 평균값과 n의 수가 많아지면 정규분포를 따름
- 이항확률분포가 푸아송확률본포로 변하는 과정



- 예시 문제

'데이터과학 > 개념 : Statistics' 카테고리의 다른 글
| [통계기초] 통계분석 : 통계적 추정 : 점추정, 구간추정 (0) | 2020.04.18 |
|---|---|
| [통계기초] 통계분석 : 통계적 추정 : 기술통계, 기본개념 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 결합확률 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 연속확률 (0) | 2020.04.17 |
| [통계기초] 확률 : 기본개념 (0) | 2020.04.16 |




