| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Python
- SQL
- R프로그래밍
- word2vec
- 데이터
- r
- 빅데이터
- 데이터처리
- 하둡
- NLP
- CNN
- 딥러닝
- ggplot
- 데이터분석
- 머신러닝
- 그래프
- R그래프
- 주가예측
- 자연어처리
- 빅데이터처리
- 데이터시각화
- HIVE
- 그래프시각화
- Hadoop
- pandas
- lstm
- R시각화
- Deeplearning
- AI
- 기계학습
- Today
- Total
욱이의 냉철한 공부
[NLP 개념정리] Word Embedding : GloVe 본문
* 자료출저 및 참고논문
- 논문
GloVe : 2014, Global Vectors for Word Representation
* Word Representation 분류체계
1. Discrete Representation : Local Representation
1) One - hot Vector
- One - hot Vector
2) Count Based
- Bag of Words (BoW)
- Document-Term Matrix (DTM)
- (TDM)
- Term Frequency-Inverse Document Frequency (TF - IDF)
- N-gram Language Model (N-gram)
2. Continuous Representation
1) Prediction Based (Distributed Representation)
- Neural Network Language Model (NNLM) or Neural Probabilistic Language Model (NPLM)
- Word2Vec
- FastText
- Embedding from Language Model (ELMo) (Bidirecional Language Model (biLM) 활용)
2) CountBased (Full Document)
- Latent Semantic Analysis (LSA)) <-DTM
3) Prediction Based and CountBased (Windows)
- GloVe
*
Discrete Representation은 값 그 자체를 표현, 정수로 표현된 이산표현
Continuous Representation은 관계, 속성의미를 내포하여 표현, 실수로 표현된 연속표현
* 목차
Word Embedding : GloVe
1. GloVe를 사용하는 이유
2. GloVe의 목적
3. "동시 등장 확률"
4. GloVe의 손실함수 식(목적식)
1. GloVe를 사용하는 이유
- 기존의 방법 1 : LSA
단어-문맥행렬에 특이값분해를 통해 데이터 차원을 줄여 잠재된 의미를 도출하는 방식
문서에서 각 단어의 빈도수를 카운트한 행렬이라는 통계정보를 입력함
-> 전체적인 통계 정보를 기반하지만, 단어간 사이의 의미(유사도)를 추출하는 성능은 떨어짐.
- 기존의 방법 2 : Word2Vec
실제값과 예측값의 오차를 손실함수를 통해 줄여나가는 학습(예측)기반의 방식
-> 단어간 사이의 의미(유사도)를 추출하는 성능은 뛰어나지만,
말뭉치 전체적인 통계 정보를 반영하지 못함. (co-occurrence)
(단순히 주변 단어 몇 개만 학습함)
- 새로운 방법 : GloVe
임베딩된 단어벡터 간 유사도 측정을 수월하게 하면서(Word2Vec의 장점) +
말뭉치 전체의 통계정보를 반영하자(LSA의 장점)
-> Word2Vec의 장점, LSA의 장점 모두 활용하자
2. GloVe의 목적
: 임베딩 된 "중심단어 벡터와 주변단어 벡터의 내적"이
전체 코퍼스에서의 "동시 등장 확률"이 되도록 만드는 것
=> 아래 식을 최소화 시키면 가능하다.

그러면 이 식은 어떻게 만들어지는 걸까 ?
3. "동시 등장 확률"

1) k = soild 일 때
ice라는 단어가 주어졌을 때 solid가 등장할 확률은 steam이 주어졌을 때 solid가 나타날 확률보다 높음.
당연히 ‘단단한’이라는 뜻을 가진 solid가 steam('증기')보다 ice('얼음')와 관련성이 높기 때문에 직관적으로 당연한 결과.
그러므로 P(solid|ice)/P(solid|steam)는 1보다 훨씬 더 큰 8.9 값
2) k = gas 일 때
gas는 ice('얼음')보다는 steam('증기')과 더 자주 등장하므로,
P(gas l ice) / P(gas l steam)를 계산한 값은 1보다 훨씬 작은 값인 0.085가 나옴.
3) k = water 일 때
solid('단단한')와 steam('증기') 두 단어 모두와 동시 등장하는 경우가 많으므로 1에 가까운 값이 나옴
4) k = fasion 일 때
solid('단단한')와 steam('증기') 두 단어 모두와 동시 등장하는 경우가 적으므로 1에 가까운 값이 나옴
4. GloVe의 손실함수 식
: 임베딩 된 "중심단어 벡터와 주변단어 벡터의 내적"이
전체 코퍼스에서의 "동시 등장 확률"이 되도록 만드는 것
- 부호 정의
X : 동시 등장 행렬(Co-occurrence Matrix)
Xij : 중심단어 i가 등장했을 때 윈도우 내 주변 단어 j가 등장하는 횟수
Xi (∑jXij) : 동시 등장 행렬에서 i행의 값을 모두 더한 값
Pik : P(k | i) = Xik/Xi : 중심 단어 i가 등장했을 때 윈도우 내 주변 단어 k가 등장할 확률
P(solid l ice) = 단어 ice가 등장했을 때 단어 solid가 등장할 확률
Pik/Pjk : Pik를 Pjk로 나눠준 값
P(solid|ice)/P(solid|steam) = 8.9
Wi : 중심단어 i의 임베딩 벡터
Wj: 중심단어 j의 임베딩 벡터
Wk : 주변단어 k의 임베딩 벡터
- GloVe 손실함수 식 도출 과정
1) 함수 F 가정
연구진들은 벡터 wi, wj, wk 를 가지고 어떠한 식, 즉 함수 F를 적용하면
Pik / Pjk 가 나온다는 가정을 세움
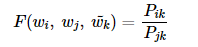
Pik / Pjk 가 의미하는 것은 아래와 같음
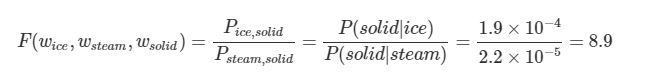
2) 함수 F의 입력 가정
우리는 함수 F가 무엇인지 찾아야 함
먼저 wi와 wj 의 차이가 함수 F의 입력으로 사용한다고 가정함

그런데 좌변은 벡터값이고, 우변은 하나의 값인 스칼라임
그래서 이를 일치하게 만들고자, F의 두 입력값을 내적함
이와 함께 단어의 의미 관계를 표현함.

3) 함수 F에 준동형(Homomorphism) 적용


* 함수 F의 3가지 조건

1. Wi와 Wk의 순서가 서로 바뀌어도 식이 같은 값을 반환
중심단어 Wk는 얼마든지 Wi나 Wj가 될 수 있기 때문.
2. 또한 말뭉치 전체에서 구한 X(co-occurrence matrix)는 대칭행렬(symmetric matrix)이므로
함수 F는 이러한 성질을 포함해야 함
3. 함수 F가 실수의 덥셈과 양수의 곱셈에 대해서 준동형(Homomorphism)을 만족
정리하면 함수 F(a+b)가 F(a)F(b)(F(a-b)가 F(a)/F(b))와 같도록 만족시켜야함

4) 함수 F : 지수함수 검증

이 식을 만족시키는 함수는 지수함수였다. 그렇기에 지수함수를 적용
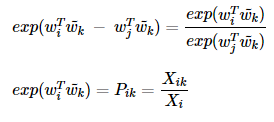
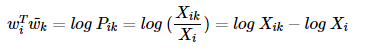
5) 식 문제점 발견
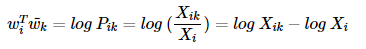
문제점 발견
함수 F의 조건 중 Wi와 Wk의 순서가 서로 바뀌어도 식이 성립되어야 한다는 것이 있었음.
그런데 이렇게 되려면 식의 log(Pik)가 log(Pki)와 같아야 함.
하지만 이것을 풀어쓰면 log(Pik) = log(Xik)−log(Xi), log(Pki) = log(Xki)−log(Xk)
Xik의 정의를 생각해보면 Xki와 같은데, 문제는 log(Xi)와 log(Xk)가 다르다...
해결책 : 상수항 (bi, bk) 적용으로 해결
그래서 해결책을 제안한다.
log(Xi)를 Wi 에 대한 편향 bi라는 상수항으로 대체
Wk에 대한 편향 bk라는 상수항으로 대체
그리하여 아래와 같은 최종식 도출한다.

6) 손실함수
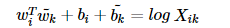
좌변의 항 (임베딩 된 "중심단어(i) 벡터와 주변단어(k) 벡터의 내적")은
우변의 값 ("동시 등장 확률")과의 차이를 최소화하는 방향으로 학습을 시켜야 한다.
그리하여 아래와 같은 손실함수 식 도출

7) 손실함수 문제점 발견

문제점 발견 : log Xik 에서 Xik 값이 0이 될 수도 있음.
해결책 : log Xik 를 log (1 + Xik)로 변경
그래도 문제점 발견 : 동시 등장 행렬 X가 Sparse Matrix일 가능성 큼
이처럼 빈도수가 낮은 값들이 많이 분포된 경우 정보에 도움을 주지 않음
해결책 : 가중치 함수 적용 f(Xik)
8) 최종 손실함수

Xik 의 값이 작으면 상대적으로 함수의 값은 작도록 하고, 값이 크면 함수의 값은 상대적으로 크도록 합니다.
하지만 Xik 가 지나치게 높다고해서 지나친 가중치를 주지 않기위해서 또한 함수의 최대값이 정함 : 최대값 1
예를 들어 'It is'와 같은 불용어의 동시 등장 빈도수가 높다고해서 지나친 가중을 받아서는 안됨



'데이터과학 > 개념 : NLP' 카테고리의 다른 글
| [NLP 개념정리] 이해하기 쉬운 분류체계 (0) | 2020.04.16 |
|---|---|
| [NLP 개념정리] Word Representation : 카운트 기반 단어표현 (0) | 2020.04.16 |
| [NLP 개념정리] Word Embedding : Word2Vec (0) | 2020.04.16 |
| [NLP 개념정리] Word Embedding : NNLM (1) | 2020.04.16 |
| [NLP 개념정리] Word Embedding 개요 (0) | 2020.04.16 |



