욱이의 냉철한 공부
[CNN 개념정리] CNN 기본개념 본문
1. computer vision
- 이미지에 신경망 적용의 문제점
이미지의 각 픽셀에 동일한 값(가중치)로 계산되어지지 않는다.
픽셀값 하나만 달라져도 다르게 계산되어진다.
즉 픽셀마다 다른 가중치(W)값을 곱해 계산한다.
이로 인해 아래와 같은 문제점이 생긴다.
1). 데이터 양 확보 어려움 : 많은 파라미터 때문에 생긴 과대 적합을 방지하도록 충분한 데이터를 얻는 것을 어렵.
2). 컴퓨터 성능 확보 어려움 : 많은 파라미터 가진 신경망을 단련하기 위한 컴퓨터, 메모리 요구사항 실행불가.
그렇다고 작은 이미지 한정해서 사용하는 것 원치 않음
그래서 나온 것이 Convolutional Neural Networks다.


- 이미지에서 우리가 원하는 기능
=> 아래 2가지가 구현되면서 파라미터 수를 대폭 줄일 수 있다.
1) trainslation invariant 해야 한다. : CNN은 Weight Sharing 한다.
다른 위치에서 동일한 feature를 추출할 수 있어야 한다.
즉 다른 위치에 있는 동일한 얼굴에서 동일한 feature를 추출할 수 있어야 한다.
예를 들어, 사진에는 동일한 객체가 다양하게 배치되어 있다.
사람이 사진 모서리에 조그만히 앉아 있어도 사람이라는 것을 알아 맞출 수 있어야 한다.
2) 위치 정보(feature)를 가지고 와야 한다. : CNN은 localed connected 되어있다.
객체의 위치가 바뀌어도 같은 Feature를 추출할 수 있어야 한다.
즉 지역적인 정보를 보고 Feature를 추출할 수 있어야 한다. 위치적 특징을 캡쳐해내야 한다.
spartial locality 정보를 반영 할 수 있어야 한다.
2. Edge detection example
- 필터의 의미
1) 필터의 수
1. Representive Capacity를 결정하는 것이다.
Feature를 다양하게 추출해야 겠다하면 이것을 늘리면 된다.
많아질 수록 다양한 Representive가 가능한 것이다.
적으면 Bottle neck 현상이 일어난다.
2. 더불어 Feature map size가 줄어드는 것에 보상이라고 할 수 있다.
2) 필터의 사이즈
지역정보를 얼만큼 가져갈것인가를 결정한다.
- 필터가 항상 홀수인 이유
ex) 3*3, 5*5
1. 짝수이면 몇 가지 비대칭적인 패딩을 가져야 한다.
2. 중앙포지션을 가지고 있는 것은 컴퓨터 비전에 있어서 특징점을 가지고 있다는 뜻
좋다. 중앙의 픽셀을 칭할 수 있고 포지션에 대해 이야기 가능.
=> 사실 전통적으로 홀수를 사용하는 의미가 더 큼.
- 필터에 3 * 3을 많이 사용하는 이유
예전에는 데이터 양과 컴퓨터 성능이 좋지 않아 아키텍쳐(Network)의 depth를 크게 가져가지 못했다.
그래서 필터가 전체 이미지 다 보기 위해서는 처음부터 필터사이즈를 크게 가져가야만 했다.
그런데 최근에는 Depth를 크게 가져갈 수 있는 환경이 구축되었다.
그리하여 필터사이즈 클 필요가 없다.
차라리 3 * 3 필터를 계속 사용하면서 Depth를 깊게 가져가자가 목표가 되었다.
이 개념과 마찬가지로, 패딩 역시 결국 Depth를 깊게 가져가기 위해 나온 것이다.
ex)11*11 1layer는 3*3 5layer와 같다.
9 * 9 1layer는 3*3 4layer와 같다.
7 * 7 1layer는 3*3 3layer와 같다.
5 * 5 1layer는 3*3 2layer와 같다.
* 왜 Depth를 깊게 가져가는가?
Representive에는 Depth가 결정적이다. Depth가 커야 high-level feuture 추출이 가능해진다.
비선형 함수의 합성함수를 통한 복잡한 함수 구현이 이를 가능하게 만들기 때문이다.
* Fully connected layer의 파라미터 수
파라미터 매우 많다. 하지면 표현력에는 Depth가 결정적이다.
비선형 함수의 합성함수로 복잡한 함수가 구현됨으로써 복잡한 문제를 해결할 수 있기 때문이다.
그리하여, 최근에는 에버리지 Pooling같은 테크닉을 사용한다.

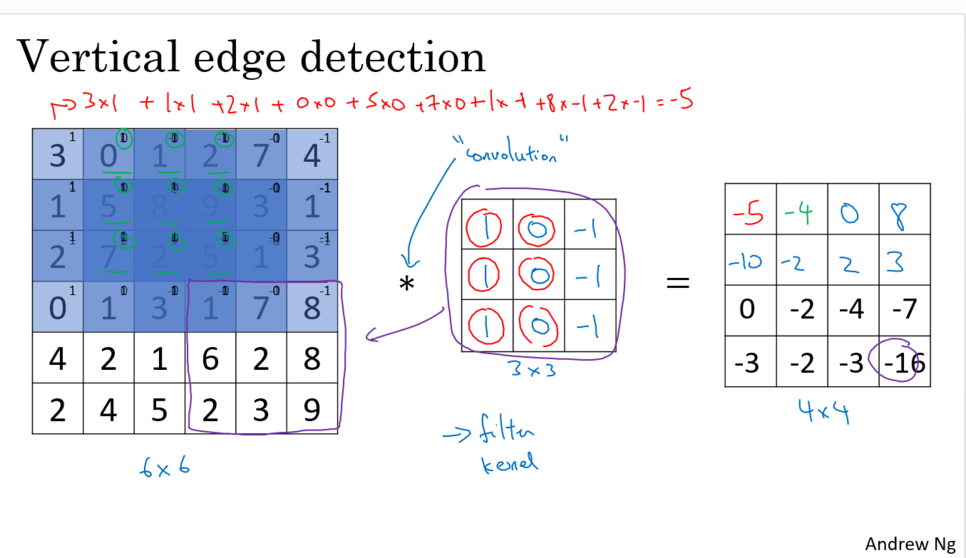

3. More Edge Detection



4. padding
- 패딩을 왜 사용하는가?
1. 컨볼루션 연산 적용할 때마다 이미지가 축소되기 때문이다.
원래 컨볼루션 연산을 하면 Feature map 크기는 축소된다.
그런데 우리는 아키텍쳐(Network)딥하게 설계하여 Representive Capacity를 크게하고, high-level feature를 추출해야만 한다.
하지만 이렇게 한다면 결국 Feature map, 즉 이미지는 축소될 것이다.
이것을 방지해야 한다.
2. 모서리에 있는 Feature(정보)를 살려야 한다.
기존은 코너나 모서리에 있는 픽셀이 아웃풋의 하나로서만 사용되도록 터치되어진다.
쉽게 말해 코너나 모서리에 있는 Feature(정보)는 적게 사용되어지고, 많이 버려지게 된다.
- 패딩 개요
패딩을 사용함으로써 Feature map 안줄어지고, Deep하게 아키텍쳐(Network)설계가 가능해졌다.
더불어 0이라는 정보 즉 노이즈를 계속 줘도, 어차피 가중치가 취사 선택하니 무시할 수 있고,
아키텍쳐(Network)는 깊게 만들어지니 더 강력해진다.
- 패딩에서 "0"의 의미
가짜값을 넣어서 학습이 잘 될 것 같지는 않다.
숫자가 있다는 것은 의미가 있는 값이다.
즉 "0" 이라는 것은 "의미 없는 정보" 라고 의미를 말해주는 것과 같다.
가중치(W)는 이 같은 정보들을 무시하게 된다.
- (필터(F) : 3, 스트라이드(Stride) : 1, 패딩(Padding) : 1) 법칙
항상 Feature map size 줄어지지 않고 그대로이다.

- 패딩을 고려한 convolutions 종류

5. Strided Convolutions
- Stride의 한 줄 의미
Special한 Feature(정보)만 추출하겠다.
- stride사용의 insight
1) stride = 1일 경우
촘촘히 봐서 모든 feature를 계산하겠다는 의미이다.
input에 가까운 layer일 수록 촘촘히 보는 것이 좋다.
이것의 장점은 모든 feature 놓치지 않고 추출하지만, 중복된 정보까지 가져올 수 있다는 것이다.
2) stride = 2일 경우
드문드문 본다. 꼼꼼하게 보지 않다.
이것의 장점은 반대로 중복된 정보를 삭제할 수 있다.



6. Convolutions Over Volume

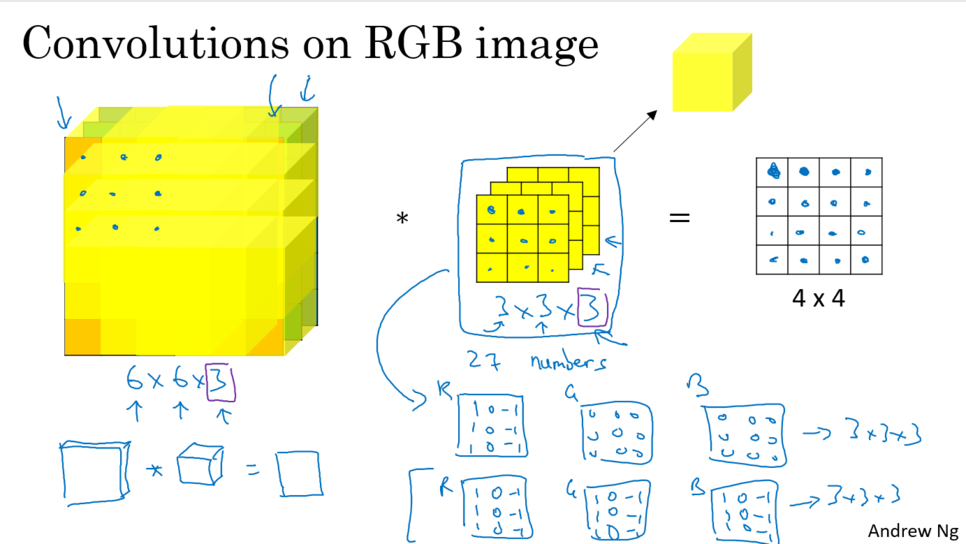

7. One Layer of a Convolutional Network
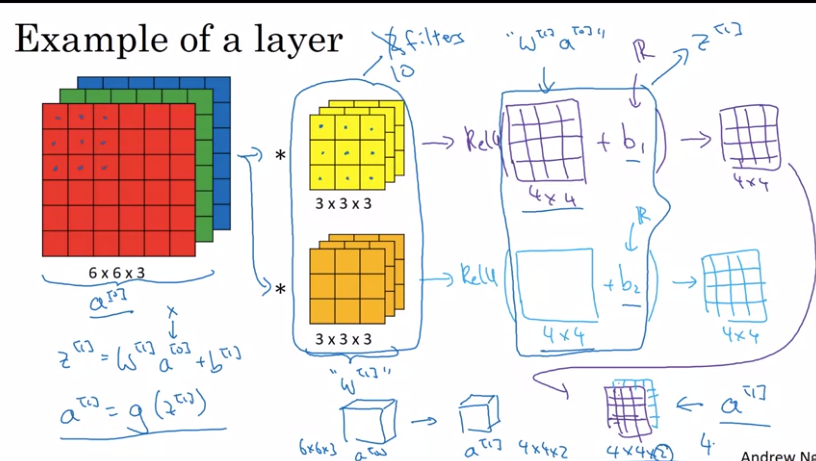

8. Simple Convolutional Network Example


9. Pooling Layers
- 풀링층의 한 줄 의미
Special한 Feature(정보)만 추출하겠다.
- 왜 풀링층을 사용하는가?
중요한 feautre, 즉 중요한 정보만 잡아두기 위해서이다.
중복되어 있는 정보들 많다. 중복된 정보들은 삭제하고 중요한 정보만 가져갈려고 한다.
예를 들어, 9라는 중요한 정보만 가지고 갈 수 있다.
더불어 Featuremap을 줄일 수 있다.
- 풀링층의 특징
1. 채널 독립적으로 연산
2. 파리미터 없기 때문에 학습되는 부분 없음.
=> 하이퍼파라미터만 수동적으로 조정하면 됨.
- Max Pooling
모델이 Deep하니 큰 시그널만 가져가겠다.
ReLU와 비슷한 역할이다.
- Max pooling과 Average Pooling 차이점
1) Max pooling
Input layer로 갈수록 필요없는 정보 혹은 중복된 정보들이 많다. noise가 많다고 한다.
이 때 Max pooling을 사용하여 Special한 정보만 가져온다.
2) Average Pooling
Output layer로 갈수록 필요한 정보 혹읜 의미있는 정보들이 많아진다.
이러한 정보들은 빠짐없이 살려야 한다.
그렇기 때문에 모든 정보들의 평균을 구하는 Average Pooling을 사용한다.
* CNN에서 각 layer마다 정보를 본다는 것
1layer마다 local하게 정보를 확인한다.
하지만 아키텍쳐(Network)가 Deep해질 수록, Output layer로 갈수록 전체를 볼 수 있게된다.



10. CNN Example


11. Why Convolutions
- 직관적인 부분 : 파라미터 수를 감소시킨다.
만약에 이것이 32*32가 아닌 1000*1000의 큰 이미지라면
생성되는 파라미터 감당 할 수 없다.
- CNN 파라미터 수
((5*5*3+1)*6) = 456
- CNN 계산량
((5*5*3+1)*6)*(28*28*6) = 2,145,024
- NN 파라미터 수
3072 * 4704 = 14,450,688
- NN 계산량
?

* 왜 적은 파라미터를 가지고 있는가? CNN의 장점
- 구체적 장점1 : 파라미터 공유
수직 에지 감지기 같은 feature 감지기가 이미지의 한 부분에서 유용하다면 이미지의 다른 부분에서도 유용 할 것이라는 견해에 따라 사용
ex) 아웃풋 모두 16 개를 계산하는 동일한 9 개의 파라미터가 파라미터 개수를 줄이는 방법 중 하나
- 구체적 장점2 : 연결의 희소성(국소 감수영역)
ex) 0(초록생 동그라미)은 9개의 인풋피쳐한테만 영향을 받는다.
=> CNN은 파라미터를 거의 가지고 있지 않고, 이는 더 작은 training cell로 훈련되고, 30 이상이 될 가능성의 더 적어짐
=> 변화불변성 잘 확인한다.
즉, 고양이의 그림이 오른쪽으로 픽셀 몇 개를 이동해도 여전히 선명한 고양이 그림이라는 것입니다.
컨볼루션 구조는 몇 픽셀 이동 된 이미지도 결국 꽤 비슷한 feature를 유지하게 하고 동일한 레이블을 지정하도록 신경망를 도와줍니다. 그리고 동일한 필터에 적용한다는 사실은 이미지의 모든 위치를 알고 있다는 것인데요, 이는 초기 레이어와 후기 레이어 둘 다에서 신경망이 더 강력해지거나 변환불변성을 바람직한 특성을 더 잘 포착하는 데 도움이 됩니다.

'데이터과학 > 개념 : CNN(OD), RNN' 카테고리의 다른 글
| [RNN 개념정리] RNN/LSTM 기본개념 (4) | 2020.06.22 |
|---|---|
| [CNN 개념정리] CNN의 발전, 모델 요약정리 2 (ResNet, DenseNet) (4) | 2020.05.01 |
| [CNN 개념정리] CNN의 발전, 모델 요약정리 1 (AlexNet ~ GoogLeNet) (1) | 2020.04.21 |



