욱이의 냉철한 공부
[통계기초] 통계분석 : 통계적 추정 : 점추정, 구간추정 본문
* 자료출저 및 참고강의
패스트캠퍼스 올인원 패키지(금융공학/퀀트) 장순용 강사님 인터넷 강의
명지대 산업경영공학과 이병기 교수님 품질관리 강의
* 목차
통계분석 : 통계적 추정(점추정, 구간추정)
1. 통계적 추정의 원리
2. 추정량의 조건
3. 구간추정
4. 구간추정 : 모표준편차를 아는 경우
5. 구간추정 : 핵심적으로 이해할 부분
6. 구간추정 : 모표준편차를 모르는 경우
1. 통계적 추정의 원리
- 통계적 추정 용어 정의
1) 점추정(point estimation)
점추정은 모수를 특정한 수치로 표현하는 것
2) 구간추정(interval estimation)
구간추정은 모수를 최솟값과 최댓값의 범위로 추정하는 것
3) 추정치(estimate)
모수를 추정하기 위해 선택된 표본을 대상으로 구체적으로 도출된 통계량
4) 추정량(estimator)
표본에서 관찰된 값으로 추정치를 계산하기 위한 도출 함수
- 예시 : 점추정과 구간추정 구분

=> 전체 20세 이상 성인의 1일 평균 수면시간을 아는 것인데, 답은 여러가지
여러가지가 점추정, 구간추정
점추정 : a와 같이 하나의 값을 제시하는 것. 추정량을 사용해서 계산
구간추정 : b,c와 같이 구간을 제시하는 것. 그런데, 구간 추정은 상황에 따라서 달라짐.
2. 추정량의 조건
- 추정량의 조건 종류
좋은 추정량이 되기 위해서는 다음과 같은 조건 충족해야 함
1) 불편성 (unbiasedness)
2) 효율성 (efficiency)
3) 일치성 (consistency)
- 추정량의 조건 : 불편성(평균)

- 추정량의 조건 : 효율성(분산)

- 추정량의 조건 : 일치성(표본크기)

- 바람직한 점추정량의 조건
1) 평균 오차제곱 : 평균 오차제곱이 최솟값이어야 함.

2) 불편성 : 추정량이 모수와 같아야 함.

3) 일치성 : 표본의 크기가 모집단 규모에 근접해야 함.
4) 효율성(유효성) : 추정량의 분산이 최솟값이어야 함.

5) 충분성 : 표본이 모집단의 대표성을 가져야 함.

3. 구간추정
- 점추정보다 구간추정을 사용하는 이유
점추정은 얼마나 정확한지 알 수가 없음
즉 조사자의 입장에서 오차를 줄이기 위해 명확한 수치를 제시하는 점추정 대신,
신뢰도를 제시하며 상한값과 하한값으로 모수를 추정하는 구간추정이 더 용이함
- 신뢰구간 정의
신뢰구간 : 표본평균의 확률분포에 모평균이 신뢰수준 확률로 포함되는 구간
상한값과 하한값의 구간으로 표시되며, 신뢰수준을 기준으로 추정된 점으로부터
음(-)의 방향과 양(+)의 방향으로 하한과 상한을 표시.



- 모평균의 구간추정
1) 구간추정 개념정리
통계량을 바탕으로 신뤼구간(confidence interval)을 계산
중심극한정리에 의하면 표본평균은 근사적으로 정규분포를 따르고 표준화된 Z는 표준정규분포를 따름.

더불어 다음과 같이 정의 가능
신뢰수준 확률 : (1-α)
오차율 : α
2) 구간추정 계산과정


4. 구간추정 : 모집단의 표준편차를 아는 경우
- 구간추정 계산방법
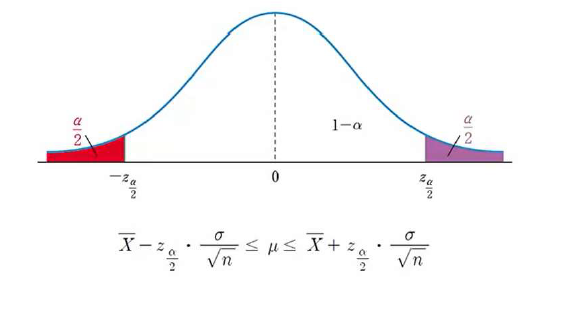
- Z에 대한 정의 : 표본정규분포의 분위수





- 문제 예시

5. 구간추정 : 핵심적으로 이해할 부분
- 모평균의 구간추정 원리
의문점을 던진다 "신뢰수준 확률이 높아야 좋은 것 아닌가?"



=> 오차율 α가 클수록 신뢰구간은 좁다. (조정 가능하지만 그대로 둠)
=> 표준편차가 작을수록 신뢰구간은 좁다. (조정 불가능)
=> 표본크기 n이 클수록 신뢰구간은 좁다. (조정 가능)
즉 표본크기를 키우면 오차율을 키우지 않고(신뢰수준 유지), 신뢰구간을 좁힐 수 있다.
- 표본크기
W가 목표하는 신뢰구간의 폭이라고 한다면, 표본크기는 아래와 같이 산정

- 표준편차와 표준오차
1) 표준편차
표본의 산포도
표본들이 흩어져 있는 산포를 뜻함
표분의 분포 특성을 확인
2) 표본오차
표본평균의 산포도
표준오차가 줄어들수록 모수 추정이 정확
6. 구간추정 : 모집단의 표준편차를 모르는 경우
- 구간추정 개념
표본의 표준편차를 이용해서 신뢰구간을 추정함.

표본표준편차를 이용한 신뢰구간은 모표준편차를 이용한 신뢰구간보다 틀릴 가능성이
더 크므로 신뢰구간 범위가 더 커질 수 밖에 없음
=> 그리하여 t분포를 사용
- 구간추정 방법

'데이터과학 > 개념 : Statistics' 카테고리의 다른 글
| [통계기초] 통계분석 : 가설검정 : 모집단 하나 (0) | 2020.04.18 |
|---|---|
| [통계기초] 통계분석 : 상관성 분석 (0) | 2020.04.18 |
| [통계기초] 통계분석 : 통계적 추정 : 기술통계, 기본개념 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 결합확률 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 연속확률 (0) | 2020.04.17 |




