욱이의 냉철한 공부
[통계기초] 통계분석 : 가설검정 : 모집단 하나 본문
* 자료출저 및 참고강의
패스트캠퍼스 올인원 패키지(금융공학/퀀트) 장순용 강사님 인터넷 강의
명지대 산업경영공학과 통계학개론 강의
* 목차
통계분석 : 가설검정
1. 가설검정 개념
2. 가설검정 : 모집단 하나일 경우 (평균차이)
3. 가설검정 : 모집단 하나일 경우 (비율차이)
4. 가설검정 : 모집단 하나일 경우 (분산차이)
1. 가설검정 개념
- 가설검정
1) 가설 (hypothesis)
주어진 사실 혹은 조사하고자 하는 사실이 어떠하다는 주장이나 추측
귀무가설 (null hypothesis) : H0
대립가설 (anti-hypothesis) : H1
2) 검정 (testing)
조사를 하기 위해 귀무가설과 대립가설을 세운 다음 어떤 가설이 맞는지를 판단해야 함
양측검정 (two-sided test) : 조사하고자 하는 대립가설, 즉 '사실이 아니다'라는 것을 검정하여 귀무가설을 기각하고 대립가설을 채택하고자 하는 것.
단측검정 (one-sided test) : 조사의 목적에 따라 대립가설을 한쪽만 살펴보는 것
3) 가설검정
모집단의 모수에 대해서 기존 통설을 가설로 하고, 표본을 추출하여 얻은 통계량으로 가설의 진위를 판단
한 차례 표본 추출 만으로 검정 (testing)
ex)
대한민국 성인 남성의 독서량은 1년에 10권
대한민국 직장인의 1년 노동시간은 2900시간이다.
- 가설검정의 의미
가설검증은 재판과 비유될 수 있다.
1) 재판
증거를 제시하기 전까지는 피고의 무죄를 전제
피고의 무죄는 증명할 필요 없음.
증명의 대상은 피고의 "유죄" 여부
판사는 "증거"에 의거해 판결을 내림.
2) 가설검정
귀무가설 (null hypothesis) : H0
모집단의 모수에 대한 통설 또는 주장 -> 피고의 무죄
대립가설 (anti-hypothesis) : H1
대립적인 주장 -> 피고의 "유죄"
- 가설검정의 요소
1) 귀무가설 (null hypothesis) : H0
2) 대립가설 (anti-hypothesis) : H1
3) 검정통계량
모수를 추정하기 위하여 표본에서 계산한 값 -> "증거"
4) p값 (유의확률)
귀무가설이 맞는다는 전제하에 계측된 검정통계량이 발생했을 확률 -> "증거"
p값이 크면 귀무가설이 맞다는 전제가 강해짐.
5) α (유의수준)
귀무가설이 사실이더라도 기각될 수 있는 최대 확률
p값에 대한 "임계치"의 역할을 함 : 판결 수준
보통 5% (0.05)를 사용
6) 1- α
사실인 귀무가설이 채택될 확률
7) 검정력(power of hypothesis testing)
허위인 귀무가설이 기각되고 대립가설이 채택될 확률
- 가설검정 순서
1) 가설수립
2) 유의수준 결정
3) 기각역 설정
4) 통계량 계산
5) 의사결정
- 가설검정 방법에 따른 순서 : 검정통계량
1) 귀무가설과 대립가설 설정
2) 검정통계량의 확률분포 결정, 검정통계량 계산
3) 유의수준 α에 해당하는 채택역과 기각역 확인
α는 보통 0.05(5%) 또는 0.01(1%)
4) 검정통계량이 채택역이면 -> 귀무가설 유지 및 채택
검정통계량이 채택역이 아니면 -> 귀무가설 기각 후, 대립가설 채택
- 가설검정 방법에 따른 순서 : p값
1) 귀무가설과 대립가설 설정
2) 검정통계량의 확률분포 결정, 검정통계량 계산
3) 유의수준 α(임계치) 설정
α는 보통 0.05(5%) 또는 0.01(1%)
4) p값 계산
(p값 > α) -> 귀무가설 유지 및 채택
(p값 < α) -> 귀무가설 기각 후, 대립가설 채택
- 가설검정 오류의 유형
오류 : 모수를 추정한 결과가 실제와는 다른 결론에 도달하는 것

2. 가설검정 : 모집단이 하나일 경우 (평균 차이)
- 가설검정 종류
1) 가설검정 종류
양측검정 (two-sided test)
우측검정 (Right-sided test)
좌측검정 (Left-sided test)
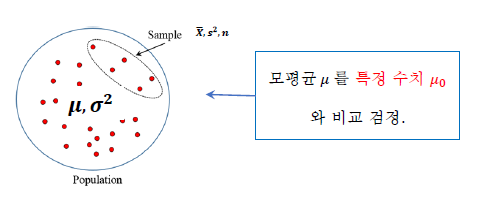
2) 모분산 사실여부에 따른 가설검정
모분산을 아는경우 : z통계량

모분산을 모르는 경우 : t통계량

z검정과 t검정의 관계

- 가설검정 : 우측검정 (Right-sided test)
0) 가설수립
H0 : 𝜇 <= 𝜇0
H1 : 𝜇 > 𝜇0

1) 가설검정 방법 : 검정통계량

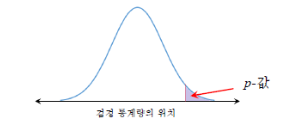
2) 가설검정 방법 : p값
검정통계량 이용하여 p값을 구한 후 α와 비교해서
p값 > α 이면 H0 유지
p값 <= α 이면 H0 기각, H1 채택
(p값 = P(Z<통계량))
- 가설검정 : 좌측검정 (Left-sided test)
H0 : 𝜇 >= 𝜇0
H1 : 𝜇 < 𝜇0

1) 가설검정 방법 : 검정통계량

2) 가설검정 방법 : p값
p값 <= α 이면 H0 기각, H1 채택
(p값 = P(Z<통계량))
검정통계량 이용하여 p값을 구한 후 α와 비교해서
p값 > α 이면 H0 유지

- 가설검정 : 양측검정 (Two-sided test)
0) 가설수립
H0 : 𝜇 = 𝜇0
H1 : 𝜇 != 𝜇0

1) 가설검정 방법 : 검정통계량
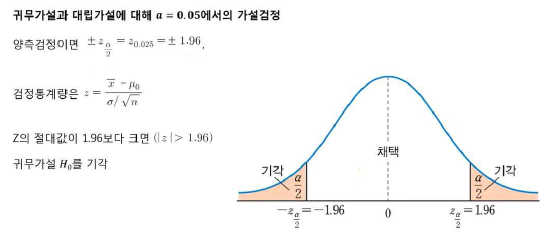
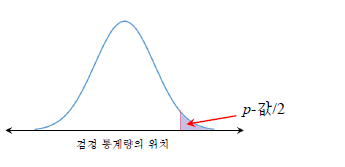
2) 가설검정 방법 : p값
검정통계량의 절대값 이용하여 p값을 구한 후 α와 비교해서
p값 > α 이면 H0 유지
p값 <= α 이면 H0 기각, H1 채택
(p값 = 2* P(Z>|통계량|))
3. 가설검정 : 모집단이 하나일 경우 (비율 차이)
0) 가설수립
표본에수 구한 비율을 p, 모집단에서의 비율을 p0라 하면,
H0 : p = p0
H1 : P != P0 (양측검정)
H1 : p < p0 혹은 p > p0 (단측검정)
1) 가설검정 방법 : 검정통계량


4. 가설검정 : 모집단이 하나일 경우 (분산 차이)
0) 가설수립
평균에 대해 어느 정도의 산포가 나타나는지를 살펴보는 가설검증이다.
H0 : σ2 = σ02
H1 : σ2 != σ02 (양측검정)
H1 : σ2 < σ02 혹은 σ2 > σ02 (단측검정)
1) 가설검정 방법 : 검정통계량


'데이터과학 > 개념 : Statistics' 카테고리의 다른 글
| [통계기초] 통계분석 : 가설검정 : 카이제곱(적합도, 독립성, 분산, 분산비) (0) | 2020.04.18 |
|---|---|
| [통계기초] 통계분석 : 가설검정 : 모집단 둘 (0) | 2020.04.18 |
| [통계기초] 통계분석 : 상관성 분석 (0) | 2020.04.18 |
| [통계기초] 통계분석 : 통계적 추정 : 점추정, 구간추정 (0) | 2020.04.18 |
| [통계기초] 통계분석 : 통계적 추정 : 기술통계, 기본개념 (0) | 2020.04.18 |




