Notice
Recent Posts
Recent Comments
Link
욱이의 냉철한 공부
[통계기초] 통계분석 : 상관성 분석 본문
* 자료출저 및 참고강의
패스트캠퍼스 올인원 패키지(금융공학/퀀트) 장순용 강사님 인터넷 강의 정리.
* 목차
상관성 분석
1. 피어슨 상관계수
2. 스피어맨 상관계수
3. 켄달 상관계수
1. 상관성 분석 : 피어슨 상관계수 (Pearson's correlation coefficient)
- 피어슨 상관계수 개요
"일상적인 상관계수"이고 다음과 같은 수식으로 계산
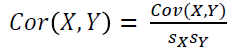
피어슨 상관계수의 값은 -1과 1사이의 수치.
피어슨 상관계수는 선형관계의 방향과 강도를 표현
Cor(X,Y) > 0 : X와 Y사이에 양의 선형관계
Cor(X,Y) < 0 : X와 Y사이에 음의 선형관계
Cor(X,Y) = 0 : X와 Y사이에 선형관계가 없음
- 피어슨 표본 상관계수의 정규분포화
표본 상관계수 r이 정규분포를 따르지 않음.
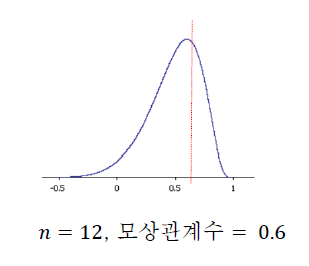
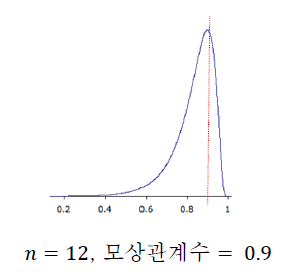
=> 변환된 수치 필요 : "피셔의 z변환"

- 피어슨 상관계수의 신뢰구간

2. 상관성 분석 : 스피어맨 상관계수 (Spearman's correlation coefficient)
- 스피어맨 상관계수 개요
X와 Y변수의 순위(rank) 사이의 상관성을 표현
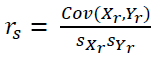
데이터에 순위만 정할 수 있다면 수치형 변수가 아니어도 적용 가능.
스피어맨 상관계수의 값도 -1과 1사이의 수치
스피어맨 상관계수는 단조로움(monotonicity)의 관계를 표현.
3. 상관성 분석 : 캔달 순위 상관계수 (Kendall's rank correlation coefficient)
- 캔달 순위 상관계수
=> (x,y) 형태로 이루어진 데이터가 있을때 i번째와 j번째 비교
부합 : (xi < xj and yi < yj) 또는 (xi > xj and yi > yj)
비부합 : (xi < xj and yi > yj) 또는 (xi > xj and yi < yj)
=> 켄달 순위 상관계수 rk는 다음과 같이 구함
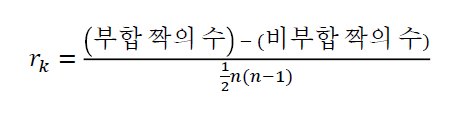
'데이터과학 > 개념 : Statistics' 카테고리의 다른 글
| [통계기초] 통계분석 : 가설검정 : 모집단 둘 (0) | 2020.04.18 |
|---|---|
| [통계기초] 통계분석 : 가설검정 : 모집단 하나 (0) | 2020.04.18 |
| [통계기초] 통계분석 : 통계적 추정 : 점추정, 구간추정 (0) | 2020.04.18 |
| [통계기초] 통계분석 : 통계적 추정 : 기술통계, 기본개념 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 결합확률 (0) | 2020.04.18 |




