| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- word2vec
- lstm
- R시각화
- 빅데이터처리
- 데이터처리
- pandas
- NLP
- Python
- 자연어처리
- 머신러닝
- 그래프시각화
- r
- R프로그래밍
- 주가예측
- R그래프
- Hadoop
- 기계학습
- SQL
- 빅데이터
- Deeplearning
- 그래프
- HIVE
- ggplot
- 데이터
- 딥러닝
- 하둡
- 데이터분석
- 데이터시각화
- AI
- CNN
- Today
- Total
욱이의 냉철한 공부
[통계기초] 통계분석 : 가설검정 : 카이제곱(적합도, 독립성, 분산, 분산비) 본문
* 자료출저 및 참고강의
패스트캠퍼스 올인원 패키지(금융공학/퀀트) 장순용 강사님 인터넷 강의
* 목차
통계분석 : 가설검정 : 카이제곱(적합도, 독립성, 분산, 분산비)
핵심)
1. 카이제곱 확률분포
2. 도수분포표(단변량)와 분할표(이변량)
3. 단병량 카이제곱 검정 : 적합도 검정
4. 이변량 카이제곱 검정 : 독립성 검정
5. 카이제곱 검정 : 분산 검정 (모집단 하나일 경우 (분산 차이))
6. F 확률분포(카이제곱/카이제곱) 검정 : 분산비 검정 (모집단 둘 일 경우 (분산 차이))
핵심)

1. 연속확률분포 : 카이제곱 확률분포(Chi Square)
- 카이제곱분포 개요
k개의 표준정규분포를 따르는 독립적인 확률변수 Xi~N(0,1)가 있을 떄,
카이제곱 확률변수 Q는 이들의 제곱의 합
k는 '자유도'라고 함

- 표현
확률변수 Q가 카이제곱 확률분포를 따른다 : Q~X2(k)
- 카이제곱 확률분포함수
카이제곱 확률분포함수는 구간 (0,+∞)에 대해서 정의

- 통계값
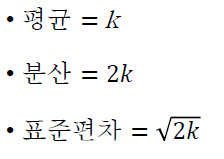
- 자유도 k의 역할
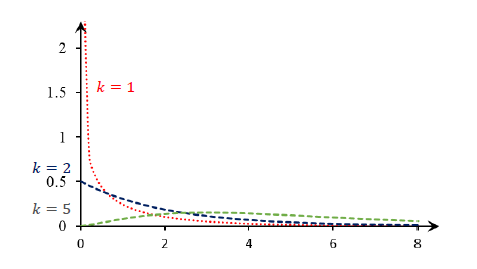
- 카이제곱 확률변수의 합
가정 : 확률변수 𝑄1와 𝑄2가 서로 독립이고, 카이제곱 확률분포를 따른다.
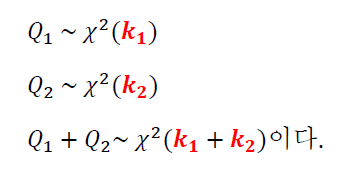

2. 도수분포표(단변량)와 분할표
1) 도수분포표 (Frequency table)
도수분포표는 한 개의 명목형(범주형) 변수가 있을 때 유형의 도수(거듭된 횟수)를 집계한 표
상대도수분포표는 도수의 상대적인 비율을 나타냄
연속형 변수를 사용하느 경우에는 구간을 설정해서 명목형 변수와 비슷하게 만듬
변수의 구간은 계급
2) 분할표 (Contingency table)
분할표는 두 개의 명목형(범주형) 변수의 도수를 정리한 표
분할표에서 도수분포표를 쉽게 구할 수 있음
|
|
남 |
여 |
합계 |
|
A반 |
40 |
60 |
100 |
|
B반 |
30 |
50 |
80 |
|
합계 |
70 |
110 |
180 |
3. 단변량 카이제곱검정(Person's Chi squared test), 적합도 검정
1) 개요
목적 : 도수분포와 모형과의 차이 여부를 밝히기 위해서 단변량 카이제곱검정 실시
적합도 검정 (goodness of fit test) 라고 부름.
두개의 유형만 있는 경우 -> 비율검정 (proportion test) 적용
2) 가설설립
H0(귀무가설) : 도수분포가 제시된 모형과 다르지 않음.
H1(대립가설) : 도수분포가 제시된 모형과 다름.
3) 가설검정 : 검정통계량

E(i) = np(i) : 모형이 제시하는 수치
O(i) : 실제 측정된 값
검정통계량은 자유도가 k-1인 카이제곱 분포를 따름
O(i)의 합은 n과 같다는 제약조건 있음
제약조건은 자유도를 감소시킴 : k-1
4. 이변량 카이제곱검정(Chi squared test in two way table), 독립성 검정
1) 개요
목적 : 분할표를 사용해서 두 변수 사이의 독립성을 검정
독립성 검정 (independence test)라고 부름
2) 가설설립
H0(귀무가설) : 두 명목형 변수느 독립적
H1(대립가설) : 두 명목형 변수는 독립적이지 않음.
3) 가설검정 : 검정통계량
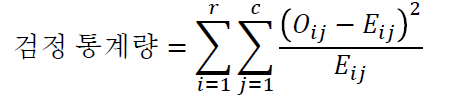
r = 행의 수
c = 열의 수
자유도가 (r-1)x(c-1)인 카이제곱 분포를 따름.
행 방향의 합과 열 방향의 합은 고정. 이것은 제약 조건
제약 조건은 자유도를 감소시킴
4) 필요성
|
|
남 |
여 |
합계 |
|
A반 |
40 |
60 |
100 |
|
B반 |
30 |
50 |
80 |
|
합계 |
70 |
110 |
180 |
반의 확률만 독립적으로 생각해보면
p(A) = 100/180
p(B) = 80/180
성별의 확률만 독립적으로 생각해보면
p(남) = 70/180
p(여) = 110/180
=>
만약에 성별과 반이 서로 독립적인 상황이라면 다음과 같이 인수분해 가능
p(반, 성별) = p(반) x p(성별)
N(반, 성별) = p(반) x p(성별) x N(tot)
= E(ij) : 변수가 독립인 경우의 기대값
그러므로 기대값 E(ij)를 실제 측정한 값 Oij와 비교하여 검정할 필요 있음.
5. 카이제곱 검정 : 분산 검정, 모집단이 하나일 경우
1) 가설수립
평균에 대해 어느 정도의 산포가 나타나는지를 살펴보는 가설검증이다.
H0 : σ2 = σ02
H1 : σ2 != σ02 (양측검정)
H1 : σ2 < σ02 혹은 σ2 > σ02 (단측검정)
2) 가설검정 방법 : 검정통계량
-> 카이제곱(n-1)을 따른다. n은 표본크기


3) 추정방법(신뢰구간)


6. F 확률분포 검정 : 분산비 검정, 모집단이 둘 일 경우
1) 가설수립
정규분포를 따르는 모집단이 두 개 있고, 이들의 분산을 비교검정
H0 : 모분산 사이에는 차이가 없음
H1 : 모분산 사이에는 차이가 있음
2) 가설검정 방법 : 검정통계량
- F 검정

* 카이제곱/카이제곱 => F 확률분포
- F 확률분포 표현
확룔변수 X가 F 확률분포를 따른다. : X~F(n(1)-1,n(2)-1)
X~F(d(1), d(2))
- 카이제곱/카이제곱 => F분포
=> 분산은 -> 카이제곱

d1은 분자의 자유도읜 n(1)-1
d2는 분모의 자유도인 n(2)-1

'데이터과학 > 개념 : Statistics' 카테고리의 다른 글
| [통계기초] 통계분석 : 가설검정 : 비모수검정 (0) | 2020.04.19 |
|---|---|
| [통계기초] 통계분석 : 가설검정 : 비모수검정 (0) | 2020.04.19 |
| [통계기초] 통계분석 : 가설검정 : 모집단 둘 (0) | 2020.04.18 |
| [통계기초] 통계분석 : 가설검정 : 모집단 하나 (0) | 2020.04.18 |
| [통계기초] 통계분석 : 상관성 분석 (0) | 2020.04.18 |




