욱이의 냉철한 공부
[딥러닝 기본] Logistic Regression as a Neural Network 본문
* 출저
본 개념정리는 제 담당교수님이신 연세대학교 정보대학원 김하영 교수님 수업과 Andrew Ng 교수님의 Coursera 수업을 통해 얻은 정보를 통해 정리했습니다. 자료는 Andrew Ng 교수님의 Coursera 수업자료입니다.
* 목차
1. Logistic Regression as a Neural Network
2. Logistic Regression 가중치 초기화
3. Logistic Regression 경사하강법
1. Logistic Regression
- Logistic Regression 개요
선형 회귀에서 금액과 채무불이행을 직선의 방정식으로 표현한다는 가설 하에, 주어진 데이터로부터 가중치 W(weight)와 편향 b(bias)를 찾아 데이터를 가장 잘 표현하는 직선을 찾았다. 그런데 이번에 배울 둘 중 하나의 선택지 중에서 정답을 고르는 이진 분류 문제(채무이행/채무불이행)는 직선으로 표현할 수가 없다.
=> 아래와 같이 확률과 선형식을 직접 연결하는 경우, 선형함수의 결과 값이 0 보다 작거나 1보다 큰 문제가 발생.
(이진분류문제의 결과값은 확률이어야 하고, 0과 1사이여야 함)
그러므로 이런 문제를 막기 위해 모든 X값에 대해 0과 1사이의 값을 제공하는 함수를 이용해야 한다.
그것이 Sigmoid 함수이다.

- 활성화 함수 : Sigmoid 함수
u = wx + b


- 통계모델링(Logistic Regression)에서의 사후확률
주어진 x 에 대한 d(실제결과값) 의 추정은 이 모델을 사용하여 posterior probability(사후 확률)를 계산한 뒤 , 그 값이 0.5 룰 넘으면
d=1, 그렇지 않으면 d=0 으로 판단한다. 즉 모델(Sigmoid함수)를 사용한 그 결과(y(x;w))는 아래와 같다.
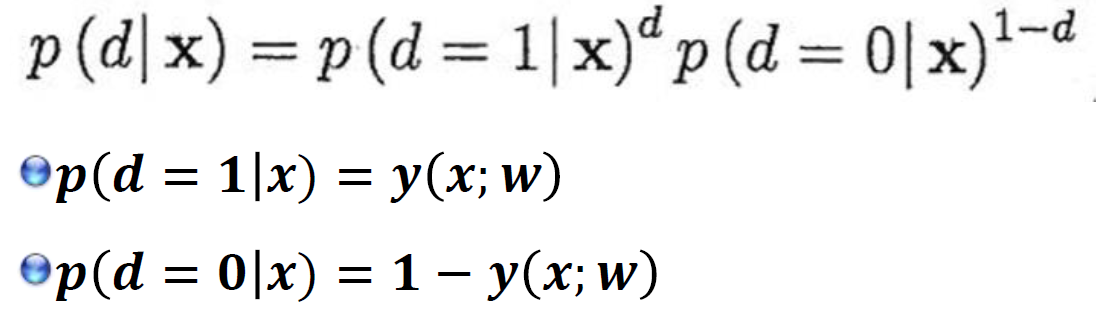
Parameter w는 training data { {(x𝒏,d𝒏)| n=1, …, N} 를 사용하여 neural network 모델로부터 얻은 사후확률 𝒑(d|x ; w)가 data가 주는 사후분포와 가장 일치하도록 학습되어진다. 여기서 이에 적합한 Parameter(w)를 추정하는 방법을 MLE(maximum likelihood estimation)이라고 한다.
MLE는 적합한 Parameter(w)를 찾기 위해 관측치로부터 구해진 아래와 같은 우도함수를 최대화 한다.

- 오차 함수 : 크로스엔트로피 (Negative log likelihood function)
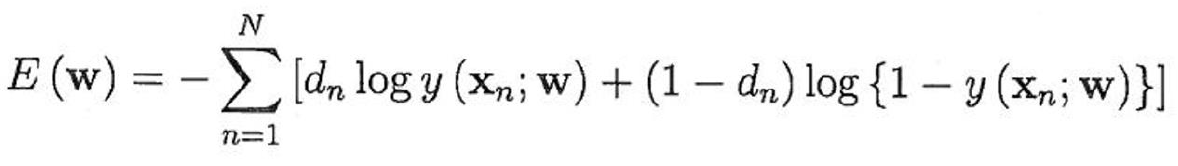
기존 MLE(최대우도함수)를 그대로 오차함수에 가져왔다. 이를 통해 최적의 Prameter(W)를 찾으며 모수의 Y분포에 예측값 Y^의 분포를 근사화 할 수 있다. 그런데 기존 MLE(최대우도함수) 식에서 달라진 점은 크게 2가지이다.
첫째, log식이 붙었다. 이유는 기존 곱셈식에서 덧셈식으로 변환되면서 계산속도를 더 빨리 가져갈 수 있다. 그리고 기존에는 결과값이 소수점까지 작게 표현되는 경우가 있겠지만, log가 붙여지면서 큰 수로 표현이 가능해졌다.
둘째, 앞에 -가 붙었다. 이것은 표현의 설득력을 위해 기존 최대화 문제에서 최소화 문제로 바꾸기 위해서이다. 오차를 최소화해야지 않겠는가.

- 크로스엔트로피 식을 사용하는 이유가 또 있는가?
오차함수로 일반 제곱오차 사용하면 비블록 문제가 있다.
그러면 경사하강법으로 전역최적값을 찾기 힘들다.
그래서 복잡한 크로스엔트로피 식을 사용한다.
- 통계모델링과 딥러닝에서의 Logistic Regression 무슨 차이인가?
똑같다. 단지 아래 Sigmoid함수 식의 u, u = wx + b를 뉴런으로 표현한 것이다. 그리고 이것을 deep하게 layer로 쌓는다면 딥러닝
Binary classification문제가 되는 것이다.

2. Logistic Regression 가중치 초기화
보통 0으로 초기화한다. 사실 어느 지점에서 초기화하더라도 똑같은 지점으로 도달한다.
왜냐하면 오차함수가 블록하기 때문이다.


3. Logistic Regression 경사하강법
- 역전파에 의한 경사 하강법
순전파 : 코스트 구한다.
역전파 : 기울기 구한다 -> 파라미터(w) 업데이트


- M개(Sample)를 모두 적용한 경사하강법


- Vectorization
딥러닝을 효율적으로 할 수 있게 해주는 방법.
for문 사용하지 않고 M개의 sample을 한 번에 계산하게 해준다.
'데이터과학 > 개념 : Deep Learning' 카테고리의 다른 글
| [딥러닝 기본] Deep Learning 학습최적화 개선 (0) | 2020.06.21 |
|---|---|
| [딥러닝 기본] Deep Learning 과적합 해결 (0) | 2020.06.21 |
| [딥러닝 기본] Deep learning 학습개념 1 (1) | 2020.06.21 |
| [딥러닝 기본] Deep Learning 배경지식 (0) | 2020.06.21 |
| [딥러닝 기본] Deep Learning 기본개념 (0) | 2020.04.17 |




