| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- word2vec
- ggplot
- pandas
- CNN
- 데이터처리
- NLP
- r
- R그래프
- 딥러닝
- 그래프
- 기계학습
- AI
- 자연어처리
- HIVE
- 데이터
- 데이터시각화
- 데이터분석
- Deeplearning
- Python
- 빅데이터
- 머신러닝
- 빅데이터처리
- 주가예측
- Hadoop
- lstm
- R프로그래밍
- SQL
- 그래프시각화
- R시각화
- 하둡
- Today
- Total
욱이의 냉철한 공부
[딥러닝 기본] Deep learning 학습개념 1 본문
* 출저
본 개념정리는 제 담당교수님이신 연세대학교 정보대학원 김하영 교수님 수업과 Andrew 교수님의 Coursera 수업을 통해 얻은 정보를 통해 정리했습니다. 자료는 Andrew 교수님의 Coursera 수업자료입니다.
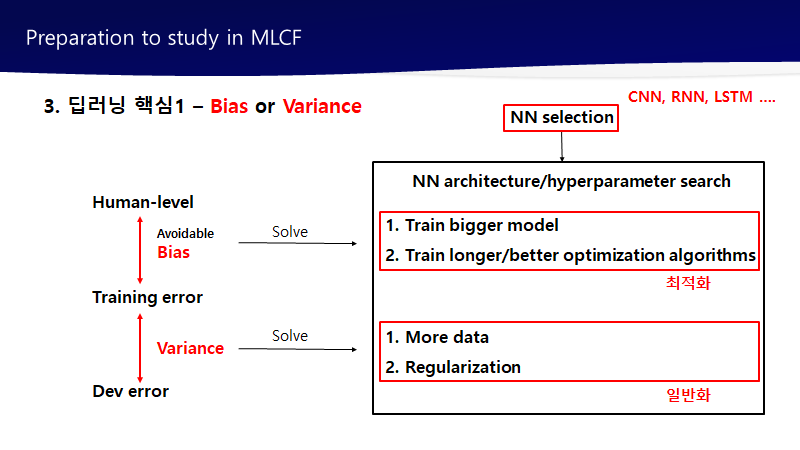

1. 딥러닝의 학습 메커니즘
- loss function의 의미
예측값과 정답과 비교하는 함수이다.
- Optimizer(옵티마이저)
loss function을 기반하여 네트워크(파라미터)를 업데이터 하는 것이다.
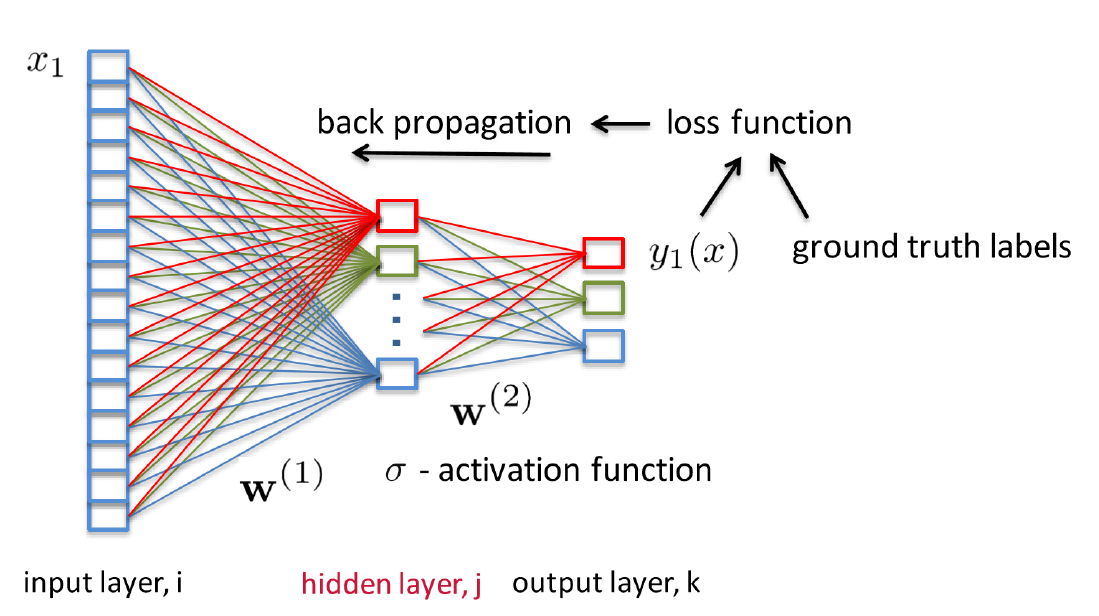
2. 학습 : 손실함수
- 활성화 함수 (Activation function)
- 손실 함수 (Loss function) 개념
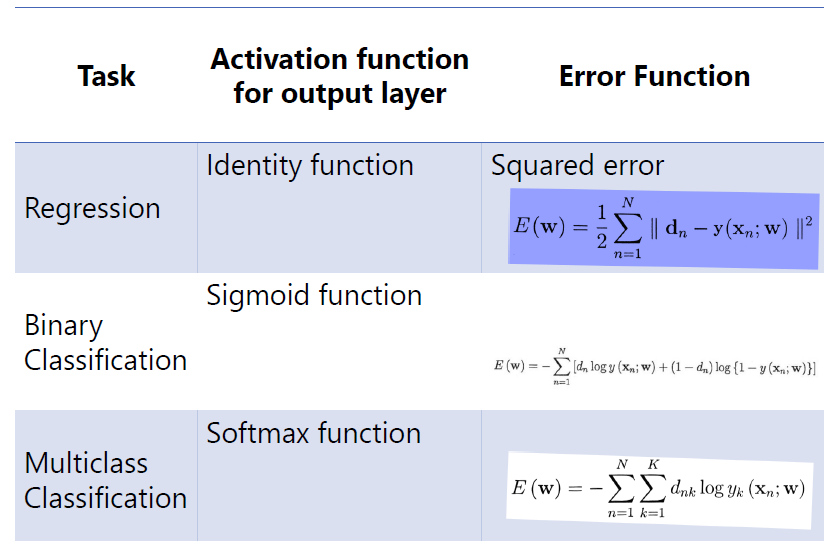
- Task 종류에 따른 손실함수 (Loss function)
1) Regression
연속값
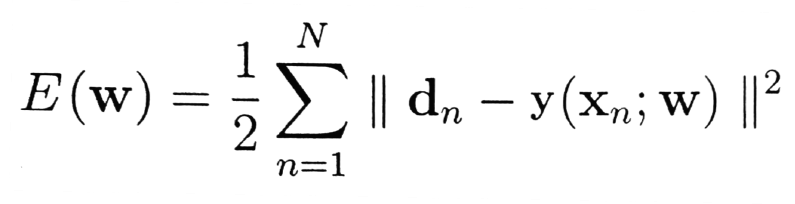
2) Binary Classification
두 종류로 구분하는 문제
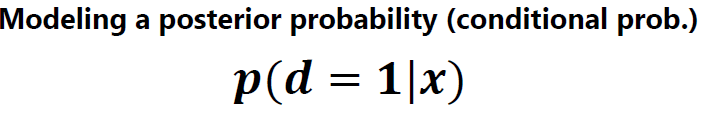
주어진 x에 대한 d의 추정은 이 모델을 사용하여 posterior probability(사후확률)을 계산환 뒤,
그 값이 0.5를 넘으면 d=1, 그렇지 않으면 d=0으로 판단
Posteriror probalility p(d = 1|x)를 모델링하는 데에 DNN을 이용.
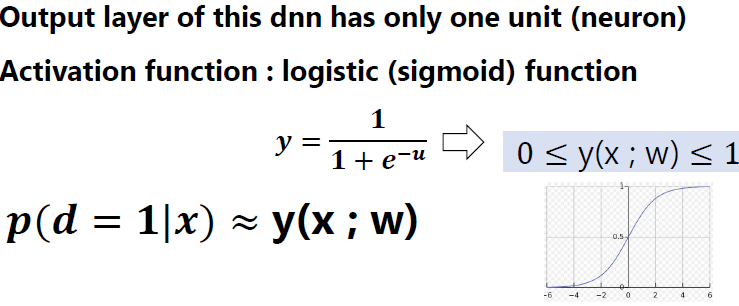
신경망의 파라미터 w를 변경함으로써 다양한 사후확률(신경망의 자유도 범위 내에서) 표현 가능
파라미터 w는 training data를 사용하여 neural network 모델로부터 얻은 posterior distribution p(d|x;w)가
data가 주는 posterior distribution과 가장 일치하도록 학습.
즉 MLE를 사용하여 파라미터 W 추정
=>
거듭제곱의 성질을 이용, P(d|x;w)을 d=1과 d=0의 posterior probability(사후확률)를 이용하면 다음과 같음
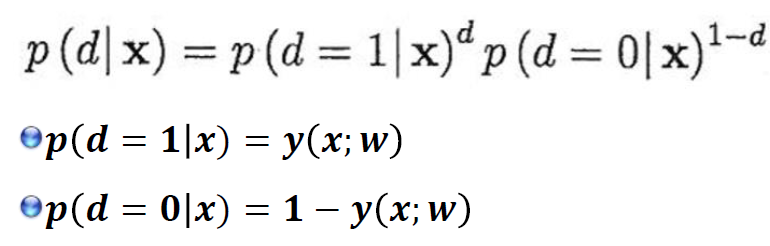
=> Likelihood Function
MLE는 관측치로부터 likelihood fuction을 최대화하는 파라미터 w 값을 추정하기 위해 사용되어진다.
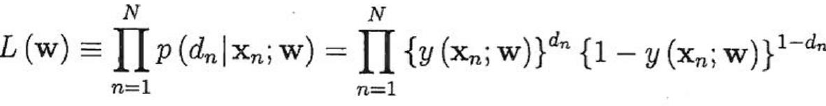
=> Negative log Likelihood(Cross-entropy) Function
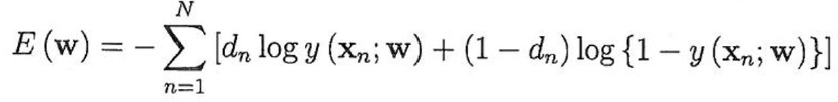
=>

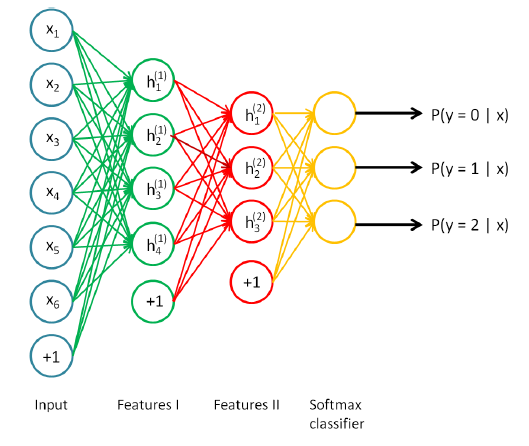
3) Multiclass Classification
Output layer l = L의 각 unit k(=1...k)의 입력은 previous layer l = L-1 의 출력에 softmax activation을 취해서 계산
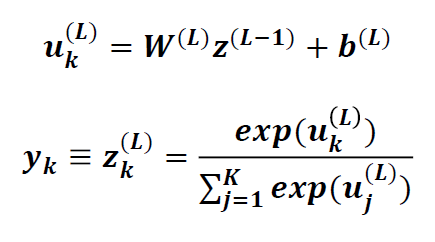
기존 activation function은 Uk만 사용해서 계산하지만 softmax function은 U1... Uk 모두 사용.
분류하는 class를 c1....ck라 한다.
Output layer의 k번째 neuron(unit)의 출력을 yk(=zk(L))은 주어진 입력 x가 class Ck에 속할 확률
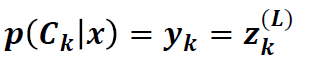
입력 x를 이 확률이 최대로 되는 class로 분류
=> Binary classification과 같이 신경망이 구현하는 함수를 각 클래스의 사후확률에 대한 함수로 간주
이런 확률모형을 기반으로 training data에 대한 신경망 파라미터(w)들의 likelihood를 평가하여
likelihood fuction이 최대가 되도록 하는 w를 찾는다.
=> Posterior probability
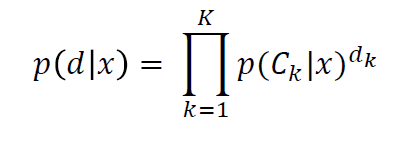
=> Likelihood function with training samples {(Xn, dn)|n=1,,,,N}
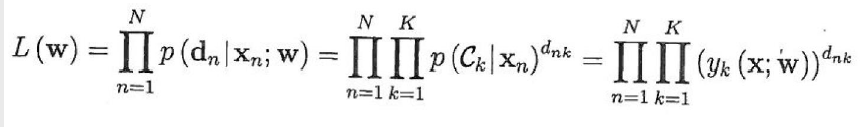
=> Cross-entropy function (negative log likelihood)
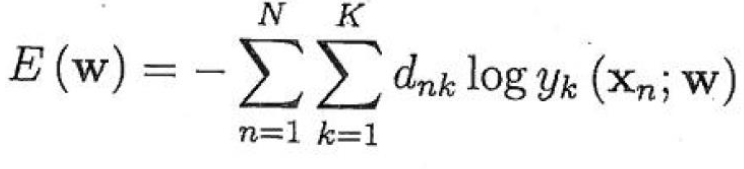
=> By difinition of conditional prob (Bayes theorem)
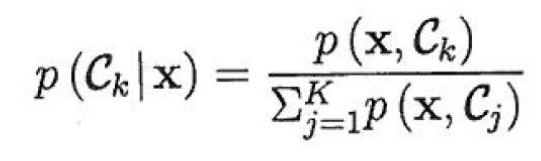
uk = log(p(x,Ck)) 라고 하면, 확률은 다음과 같다.
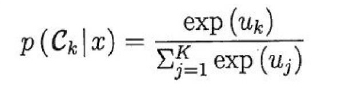
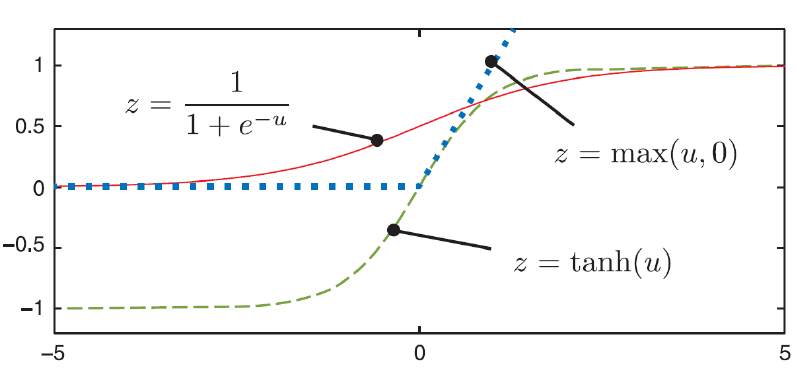
3. 학습 : 활성화 함수 (Activation function)
- 활성화 함수 (Activation function) 개념
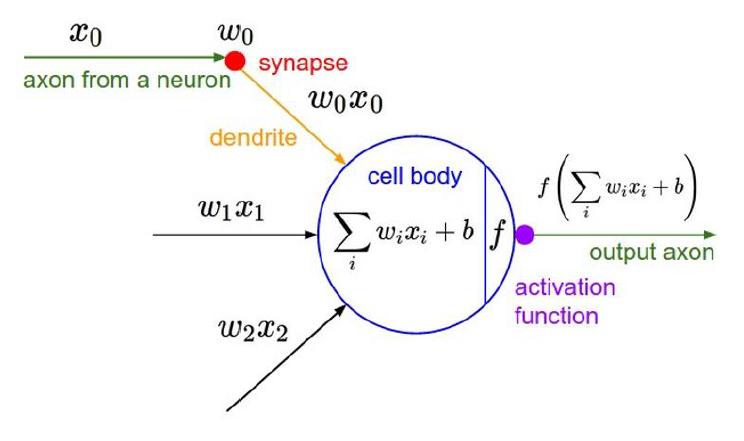
- 활성화 함수 (Activation function) 종류
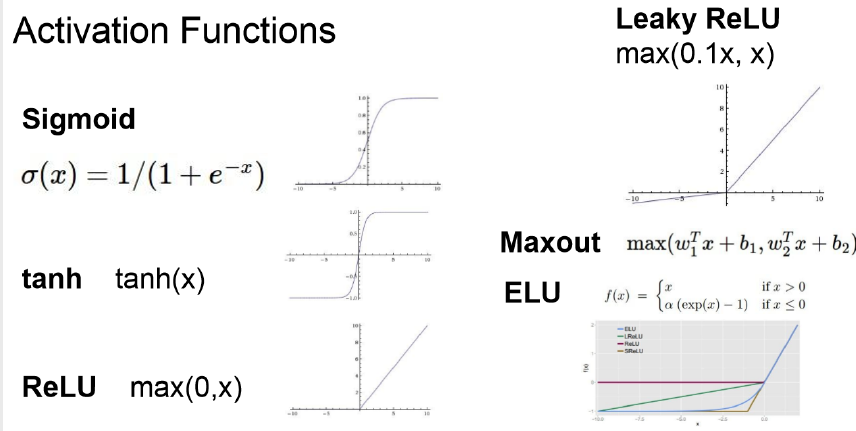

1) Sigmoid function
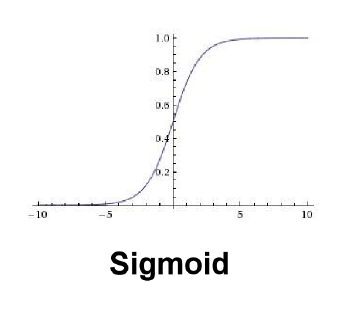
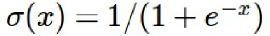
1. 특징
범위는 0 ~ 1
Sigmoid function은 이진분류를 위해 마지막 활성화 층에 사용할 때만 주로 사용
2. 문제점
1) 기울기 가장 큰 부분은 1/4
기울기가 0인 부분은 역전파 할 때 기울기 소실 문제 발생
2) Output이 0에 집중되지 않는다.
3. 해결책
문제점을 해결하고자 등장한 함수가 Relu
2) 쌍곡선 함수(tanh)
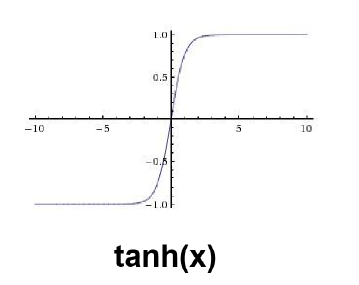
1. 특징
범위 –1 ~ 1
시그모이드 함수 평행이동 시킨 것과 같다.
2. 장점
기울기가 가장 큰 부분이 1이며, 학습성능이 sigmoid보다 더 좋다.
Output이 0이 아닌 0.5로 집중화
이렇게 함으로써 다음 층의 학습이 더 쉽게 이루어짐, 즉 최적화에 이점
3. 단점
1) 기울기 가장 큰 부분은 1/4
기울기가 0인 부분은 역전파 할 때 기울기 소실 문제 발생
4. 해결책
이것을 해결하고자 나온 함수가 Relu
3) Relu 함수
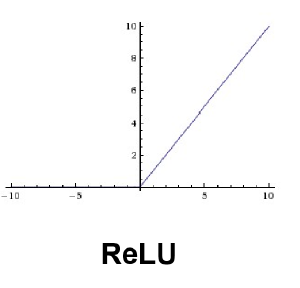

1. 특징
식이 단순하기 때문에 계산 빠르며, 효율적이다.
학습속도 또한 빠르기 때문에 빠르게 수렴된다.
더불어 0 이상에 기울기 값 다 가지고 있기 때문에, 기울기가 사라지지 않는다.
2. 문제점
음수일 때는 기울기값이 0으로, 기울기가 사라진다.
4). Leaky ReLu 함수
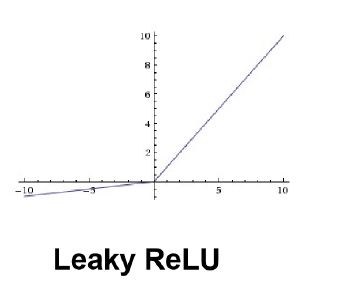

1. 특징
식이 단순하기 때문에 계산 빠르며, 효율적이다.
학습속도 또한 빠르기 때문에 빠르게 수렴된다.
더불어 0 이상에 기울기 값 다 가지고 있기 때문에, 기울기가 사라지지 않는다.
2. 장점
0 이하일 때도 죽지 않는다.
5) ELU : Exponential Linear Units
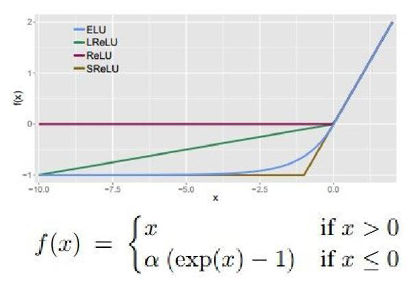
1. 특징
=> ReLU의 이점 가지고 있다.
(식이 단순하기 때문에 계산 빠르며, 효율적이다.
학습속도 또한 빠르기 때문에 빠르게 수렴된다.
더불어 0 이상에 기울기 값 다 가지고 있기 때문에, 기울기가 사라지지 않는다.)
=> 죽지 않는다.
=> 아웃풋이 제로평균에 가깝다.
2. 문제점
0 이하일 때는 exp() function을 사용하기 때문에 계산량 많아진다.
4. 학습 : 활성화 함수 (Activation function) 필요성
- 의미
Hidden layer에 비선형함수를 사용함으로써 복잡한 함수가 되며 이것은 표현력이 더 좋아지는 이유가 된다.
그렇기 때문에 Deep learning으로써의 의미가 생긴다.
- 만약에 은닉층에 선형함수를 사용한다면?
로지스틱(즉 1층)하고 다를 바가 없다.
2개 선형 합쳐도 선형
아무리 층을 깊게해도 결과는 선형이다.
즉 의미가 없다...
'데이터과학 > 개념 : Deep Learning' 카테고리의 다른 글
| [딥러닝 기본] Deep Learning 학습최적화 개선 (0) | 2020.06.21 |
|---|---|
| [딥러닝 기본] Deep Learning 과적합 해결 (0) | 2020.06.21 |
| [딥러닝 기본] Deep Learning 배경지식 (0) | 2020.06.21 |
| [딥러닝 기본] Logistic Regression as a Neural Network (0) | 2020.04.25 |
| [딥러닝 기본] Deep Learning 기본개념 (0) | 2020.04.17 |




