욱이의 냉철한 공부
[딥러닝 기본] Deep Learning 과적합 해결 본문
* 출저
본 개념정리는 제 지도교수님이신 연세대학교 정보대학원 김하영 교수님 수업과 Andrew 교수님의 Coursera 수업을 통해 얻은 정보를 통해 정리했습니다. 자료는 대부분 Andrew 교수님의 Coursera 수업자료입니다.
* 목차
1. 과적합(Overfit) 해결 : Regulation(규제화)
2. 과적합(Overfit) 해결 : Drop-out(드롭아웃)
3. 과적합(Overfit) 해결 : data augmentation
4. 과적합(Overfit) 해결 : early stopping
5. 과적합(Overfit) 해결 : 모델 Size를 축소?

1. 과적합(Overfit) 해결 : Regualtion(규제화)
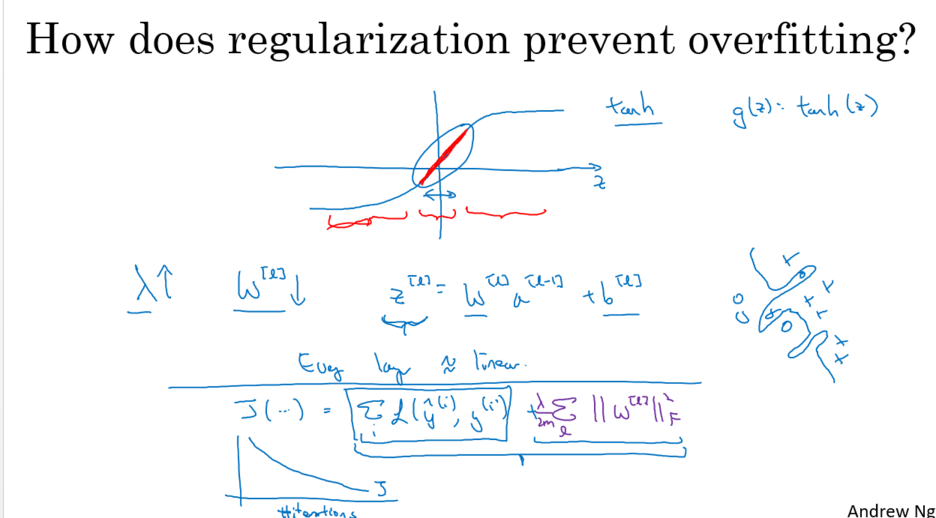
- Regulation(규제화)가 왜 Overfit(과적합)을 해결하는가?
가중치(W) 즉 자유도에 제약을 건다.
학습할 때 가중치(W)값을 0에 가깝게 한다. 즉 Sparse하게 만든다고 할 수 있다.
가중치(W)값이 작아지면서, Z값이 작아지고, 활성화 함수가 선형수에 근접하게 된다.
예시로 Tanh 활성화 함수를 보면, 가운데(0)으로 갈수록 선형함수화 되는 것을 확인할 수 있다.
Regulation(규제화)를 사용하면 가중치(W)값이 작아지면서, Z값도 0으로 향하기 때문에 선형함수화 되는 것을 확인 할 수 있다. 즉 복잡한 함수가 아닌 간단한 함수가 된다. => 일반화 효과
이것은 모델 크기를 줄이는 것과 같은 효과이다.


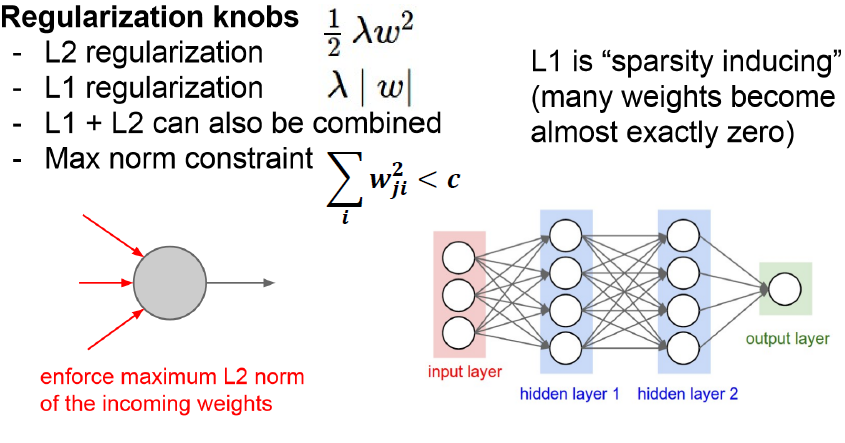
- Regulation(규제화) 종류
1) L1 Regulation(규제화)
L1 Regulation은 대부분의 가중치(W)를 0으로 만든다. 이를 통해 모델을 Sparse하게 만든다.
이것은 반면 어떤 특성들이 모델에 영향을 주고 있는지 정확히 판단해준다.
2) L2 Regulation (규제화)
L2 Regulation은 L1 Regulation과 다르게 가중치(W)들의 제곱을 최소화하므로, 가중치(W)의 값이 완전히 0이 되기보다 0에 가까워지는 경향을 가지고 있다.
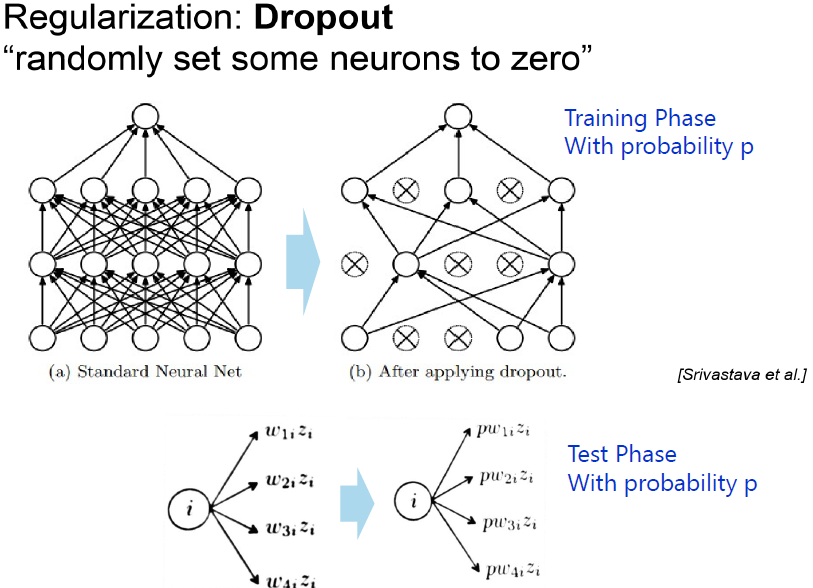
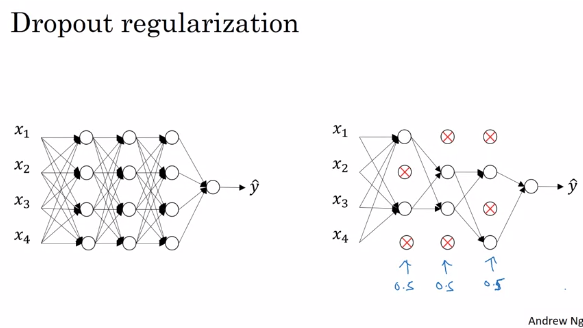
2. 과적합(Overfit) 해결 : Drop-Out(드롭아웃)
- 드롭아웃(Drop-out) 개요
-> W 분산시켜서 다양성 추구, 여러 가지 모델 학습하는 효과 가져온다.
-> 랜덤하게 계속 재설정, 미니배치 사용한다면 배치마다 가중치는 드롭아웃 적용되서 업데이트
-> 입력층, 출력층은 바꾸지만 않다.
-> 반복할 때마다 더 작은 신경망으로 일하는 것과 같음
- 드롭아웃(Drop-out) 설명
미니배치마다 각 layer마다 확률을 넣어 Neuron의 활성화 멈추게 한다.
그리하여 매 미니배치마다 다른 아키텍쳐(Network)를 학습하게 만드는 구조이다.
이것은 과적합을 막게 한다. 구체적인 설명은 다음과 같다.
1) 규제화 효과
반복할 때마다 작은 신경망으로 학습이 되며, 매번 활성화되는 Neuron이 달라지기 때문에 헷깔리게 만든다.
이것은 한가지 Neuron 즉 한가지 Feature에 많은 비중을 부여하지 않는 효과가 있다.
어느 특정 Neuron이 큰 가중치 값을 가져서 큰 영향력을 행사하지 않는다는 뜻이다.
이를 통해 규제화 효과를 가져오게 된다.
2) 앙상블 효과
매 미니배치마다 여러가지 모델(다양성) 학습하게 된다.
원래 신경망을 학습하게 되면 각 미니매치마다 Overfitting이 일어난다.
그런데 미니배치마다 다른 모델이 학습되다보니, 여러 모델이 합쳐져 Voting에 의한 평균 효과로
Overfitting이 상쇄되는 regularization과 비슷한 효과를 가져온다.
- 드롭아웃(Dropout)과 L2 Regulaltion의 차이점
1) L2 Regulation (규제화)
노이즈 작은 것에 사용
2) 드롭아웃(Dropout)
노이즈 큰 것에 주로 사용(CNN에서 강력한 기법)
ex) 컴퓨터비전에서 입력값 크기가 너무 커서 모든 픽셀들을 입력하는 데에는 항상 데이터 부족하다.
이럴 때 드롭아웃 사용한다.


3. data augmentation
- data augmentation 개요
이미지에서 자주 사용 (CNN에서 강력한 기법)
너무 심한 방향전환은 금물이다.
ex) 숫자 8을 오른쪽으로 회전하면 무한대 기호가 될 수 있다.
- data augmentation 주의할 점
TEST set에서는 Data augmentation 사용하면 안된다.
TEST set은 노이즈 없는 정확한 데이터 사용해야 한다.
- data augmentation 단점
관계형 데이터테이블에서 사용 어렵다.
즉 적용하기 까다롭다.

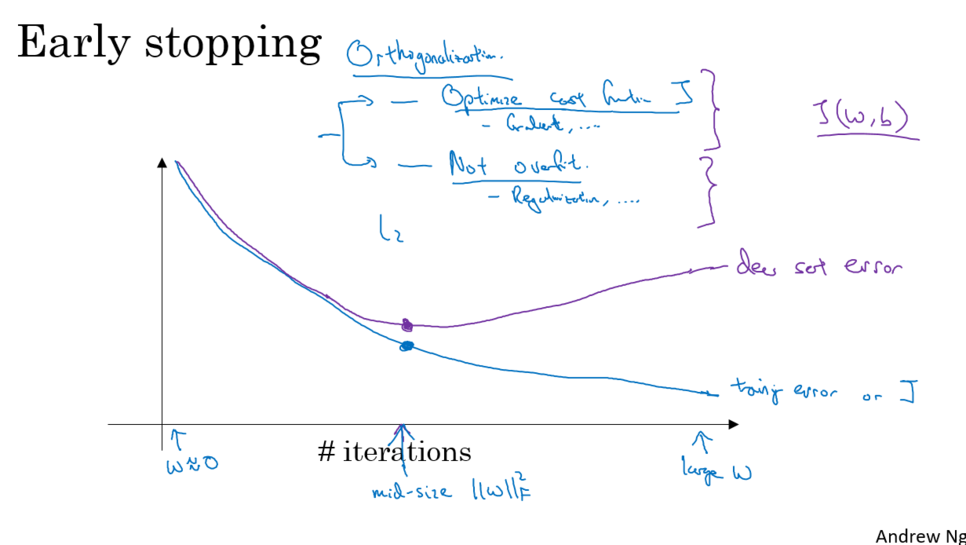
4. early stopping
- early stopping 사용에 고민해야할 부분
eqrly stopping은 과적합 방지의 좋은 방법
하지만 최적화 <-> 과적합 사이에서 고민해야 한다.
우리는 최적화를 높이고 과적합을 줄여야 한다.
early stopping은 이 둘 사이를 복잡하기 만드는 경향이 있다.
5. 과적합(Overfit) 해결 : 모델 Size를 축소?
- 모델 Size 축소는 최후의 보류
모델(Network) Size를 줄이는 것은 되도록 사용하지 않는다.
왜냐하면 모델의 자유도(Neuron의 수)가 축소되고, 이것은 Representive Capacity가 축소되는 것과 같다.
이렇게 된다면, High-level Feature의 학습이 어렵게 되고, 성능이 좋게 개선되지 않는다.
다른 말로 설명하자면 함수들을 합성하면서 더 복잡한 함수로 표현하는 것에 제약이 걸리고, 더 복잡한 문제를 해결하는 것에도 제약이 걸리는 것과도 같다.
'데이터과학 > 개념 : Deep Learning' 카테고리의 다른 글
| [딥러닝 기본] Deep Learning 핵심개념 : Feature추출에 대한 이해 (1) | 2020.06.22 |
|---|---|
| [딥러닝 기본] Deep Learning 학습최적화 개선 (0) | 2020.06.21 |
| [딥러닝 기본] Deep learning 학습개념 1 (1) | 2020.06.21 |
| [딥러닝 기본] Deep Learning 배경지식 (0) | 2020.06.21 |
| [딥러닝 기본] Logistic Regression as a Neural Network (0) | 2020.04.25 |



