욱이의 냉철한 공부
[딥러닝 기본] Deep Learning 배경지식 본문
* 출저
본 개념정리는 제 담당교수님이신 연세대학교 정보대학원 김하영 교수님 수업과 Andrew 교수님의 Coursera 수업을 통해 얻은 정보를 통해 정리했습니다. 자료는 Andrew 교수님의 Coursera 수업자료입니다.
1. Tensor 개념
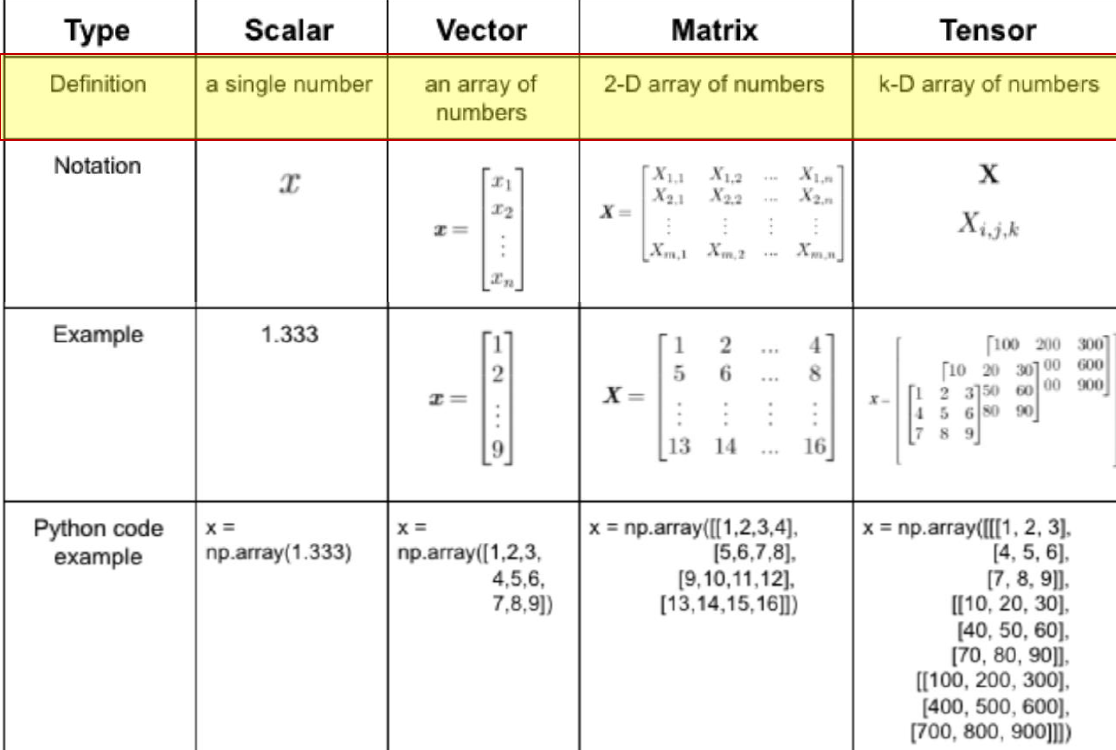
2. MLE(Maximum likelihood estimation) 개념
- Maximum likelihood estimation(MLE) 개념
원래 모집단의 분포에 최대한 가깝게 파라미터를 추정하는 방법.
머신러닝의 목표는 미지의 데이터에(아직 확인하지 않은 데이터)에 대해 좋은 예측을 하는 것이다.
즉 데이터를 잘 설명할 수 있거나, 주어진 데이터로부터 결과값을 잘 예측하는 것들이 이에 속한다.
이것을 일반화라고 한다. (generation)
좋은 일반화(generation) 성능을 얻기 위해서 우리는 알고자 하는 실제 확률 분포(모집단의 분포)로부터
데이터를 수집(샘플링)하고, 수집된 데이터를 가장 잘 설명하는 확률 분포 모델을 추정함으로써,
알고자 하는 실제 확률 분포를 근사한다.

- Log를 취하는 이유
1) 굉장히 작은 값도 구체적인 표현이 가능.
2) 곱셈을 덧셈으로 바꾸면서, 연산량을 줄일 수 있음.
3) 가우시안 분포에서 지수를 제거 할 수 있음.
- Maximum likelihood estimation(MLE)가 딥러닝에서의 역할
지금까지 가능도 이야기를 한 이유는 신경망 또한 확률 분포 함수이기 때문
Multi-classfication 문제를 풀고자 하는 경우 0부터 n까지이 레이블(클래스)를 예측하게 되므로
이산 확률 변수를 다루는 멀티눌리 분포가 된다.
따라서 이 문제를 위해 신경망의 마지막 layer에서 소프트맥스 연산 y의 결과값은
클래스별 확률값에 대한 분포 y^을 봔환한다.
실제 정답레이블 y의 경우에는 불연속적 값이기 때문에 원핫 벡터가 된다.
달리 말하면 y도메인의 샘플은 이산확률분포 P(y)에서 샘플링한 샘플이기 때문에 원핫 벡터로 표현

3. Information content(정보량) 개념
- Information content(정보량) 개념
정보이론이란 데이터를 정량화하기 위한 응용 수학의 분야
그리하여 정보이론 또한 신경망과 밀접한 연관이 있음.
흔히 쓰는 표현인 정보량은 불확실성 또는 놀람의 정도를 나타냄.
일어날 확률이 낮을수록 불확실성이 높고, 일어났을 때 놀람이 커질 것이기 때문에,
정보량이 높다는 것은 어떤 일이 일어날 확률이 낮은 것을 의미.
예를 들어 누구나 뻔히 예측 할 수 있는 것은 작은 정보로도 표현 가능.
- Information content(정보량) 수식
일어날 확률이 낮을수록 많은 정보 갖고 있음.

- 엔트로피(entropy) 개념 및 수식
정보량에 평균(기대값) 취하면 엔트로피(entropy)라고 함.
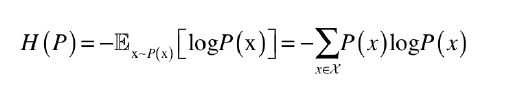
이 때, 엔트로피(entropy)는 분포의 대략적인 모양이 얼마나 퍼져있는지 뾰족한지 가늠하는 척도
보통 엔트로피(entropy) 작으면 작을수록 그 분포는 뾰족한 모양.
뾰족한 확률 분포일수록 특정 값에 대한 확률이 높다는 뜻.
- 교차 엔트로피(cross entropy) 개념 및 수식
분포 함수 P에서 샘플링한 x를 통해 분포 함수 Q의 평균 정보량을 나타낸 것
교차라는 단어에서 알 수 있듯이, 다른 분포 P를 사용하여 대상 분포 Q의 엔트로피 측정
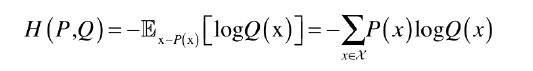
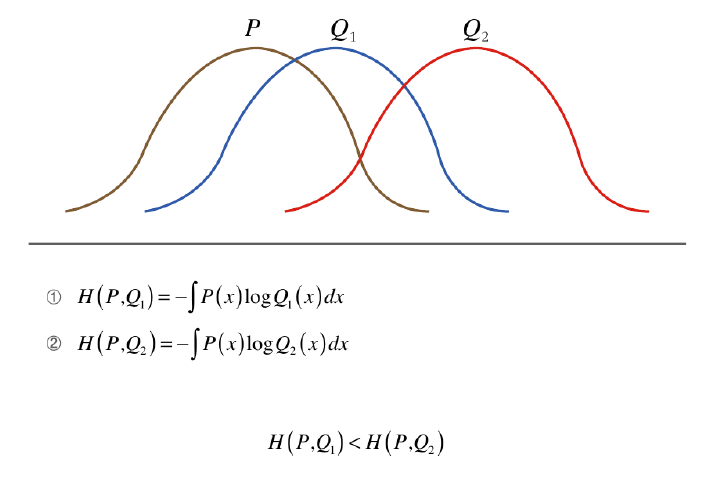
-log를 취했기 때문에, 분포 P와 Q가 비슷한 모양일 수록 교차 엔트로피는 더 작은 값.
그러므로 그 동안 분류 문제에서 교차 엔트로피 손실 함수를 사용하여,
손실 함수의 값이 최소가 되도록 경사하강법을 통해 신경망 훈련해온 것.
즉 알아내고 싶은 실제 확률 분포 P에서 샘플링한 데이터 x를 통해 신경망으로 구성된 확률 분포
PΘ 에 넣어 교차 엔트로피가 최소가 되도록 경사하강법 수행.
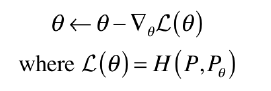
다만, 이것은 값을 통해 바로 확률값을 구할 수 있는 이산확률변수를 다루는 확률분포에만 해당
보통 연속확률분포의 경우는 MSE(평균제곱오차) 손실함수를 통해 훈련(학습)
연속 확률 분포의 경우 교차 엔트로피를 적용하는 것이 틀린 내용이 아니지만,
샘플에 대한 확률값을 구할 수 없기 때문에, 그것이 가능한 이산확률분포에만 교차 엔트로피 수행
4. Kullback-Leibler divergence 개념
- Kullback-Leibler divergence 개념

KLD는 두 분포 사이의 괴리를 보여준다.
수식 내에서 분포 P와 분포 Q의 위치에 따라서 KLD의 값은 달라질 수 있으므로,
대칭의 개념이 아니기에 '거리'라고 표현하지는 않는다.
따라서 두 분포 사이의 차이를 줄이고자 할 때, KLD를 최소화 하는 것은 매우 좋은 전략
그렇다면 교차 엔트로피 대신에 신경망 훈련(학습)위해 KLD를 사용하면 되지 않는가?
사용하고 있다!

KLD에 신경망 파라미터 Θ로 미분하여 보면 교차 엔트로피와 같은 미분 결과값 도출된다.
따라서 교차 엔트로피를 손실 함수로 활용하여 경사하강법 하는 것과,
KLD를 손실함수로 활용하여 경사하강법 하는 것은 같다.
5. Cross entropy = log likelihood ??
- Cross entropy

- log likelihood

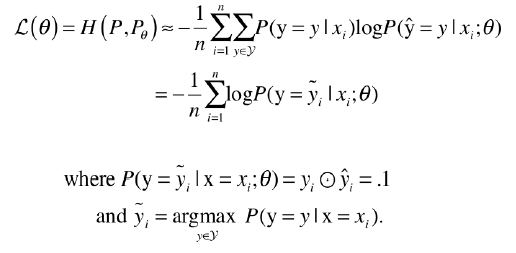
'데이터과학 > 개념 : Deep Learning' 카테고리의 다른 글
| [딥러닝 기본] Deep Learning 학습최적화 개선 (0) | 2020.06.21 |
|---|---|
| [딥러닝 기본] Deep Learning 과적합 해결 (0) | 2020.06.21 |
| [딥러닝 기본] Deep learning 학습개념 1 (1) | 2020.06.21 |
| [딥러닝 기본] Logistic Regression as a Neural Network (0) | 2020.04.25 |
| [딥러닝 기본] Deep Learning 기본개념 (0) | 2020.04.17 |




