| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- R시각화
- 자연어처리
- NLP
- lstm
- Python
- AI
- Hadoop
- 빅데이터
- 그래프시각화
- r
- 데이터시각화
- 빅데이터처리
- 딥러닝
- 주가예측
- 머신러닝
- R프로그래밍
- SQL
- 데이터
- Deeplearning
- R그래프
- pandas
- 하둡
- 그래프
- ggplot
- 데이터처리
- word2vec
- HIVE
- 기계학습
- 데이터분석
- CNN
- Today
- Total
욱이의 냉철한 공부
[통계기초] 확률변수와 확률분포함수 : 연속확률 본문
* 자료출저 및 참고강의
패스트캠퍼스 올인원 패키지(금융공학/퀀트) 장순용 강사님 인터넷 강의
명지대 산업경영공학과 박윤선 교수님 통계학개론 강의
*목차
1. 연속확률
2. 연속확률분포 : 연속균등분포(Uniform distribution)
3. 연속확률분포 : 정규확률분포
4. 연속확률분포 : 표준정규확률분포
5. 연속확률분포 : 지수 확률분포(Exponential)
6. 연속확률분포 : 카이제곱분포(Chi Square)
7. 연속확률분포 : 스튜던트 t 확률분포 (Student t)
8. 연속확률분포 : F 확률분포
1. 연속확률
- 연속확률변수 (continuous random variable)
셀 수 없는(무한대) 가지수의 값을 가지는 확률변수
어떤 실선 구간에 있는 점들에 대응하는 무한히 많은 값들을 부여
ex) 신장, 높이, 무게, 제품수명, 실험에서의 에러
- 연속확률변수 특징
확률은 구간에 대해서 정의.
즉 P(X=x0)와 같이 특정 위치에 대한 확률은 의미가 없고,
P(x1<=X<=x2)와 같이 X가 어느 구간에 있을 확률이 의미가 있음.
- 연속확률밀도(연속확률분포)

이 부드러운 곡선이 연속확률변수의 확률분포.
연속확률변수는 실선 위의 무수히 많은 값들 중 임의의 값을 취할 수 있음.
확률의 밀도(density)를 확률변수 X에 대한 확률분포(probaility distribution)
또는 확률밀도함수(probaility density function)이라고 하며, 수학적 기호 f(x)로 표기.
이산확률분포함수와는 다르게 이것 자체만으로는 확률의 의미가 없음.
연속확률밀도를 사용하여 연속확률변수의 값이 특정 구간에 속할 확률을 표현 가능.
연속 확률분포함수 또는 확률밀도함수를 f(x)와 같이 표기하여 구간의 확률 P(x)와는 구분
- 연속확률밀도 특징

1) f(x0)에는 확률의 의미가 없음.
2) P(x1 <= X <= x2)와 같이 X가 어느 구간에 있을 확률이 의미가 있음.
3) 0 <= f(x)
4) f(x)가 정의되어 있는 구간에서 f(x) 아래의 총 면적은 1과 같아야 함.
2. 연속확률분포 : 연속균등분포(Uniform distribution)
- 연속균등분포 개요
연속 균등확률분포함수는 구간 [a,b]에 대해 정의.
이외의 구간에서는 f(x) = 0 이다.

확률밀도가 균등하기 때문에 확률은 구간 [x1,x2]의 폭에 비례.

- 표현
확률변수 X가 연속균등확률분포를 따른다 : X~Unif(a.b)
- 통계값

- 연속균등분포의 누적확률 (Cumulative Distribution Function, CDF)
연속균등분포의 누적확률 𝐶𝐷𝐹(𝑥)는 구간 (−∞,𝑥] 에서 𝑓(𝑥) 아래의 면적과 같음
즉, 𝐶𝐷𝐹(𝑥)=𝑃(−∞<𝑋≤𝑥)

CDF(x)는 x가 증가하면 1로 수렴.

- 예시 문제

3. 연속확률분포 : 정규확률분포
- 정규분포함수
정규분포함수는 구간 (−∞,+∞)에 대해서 정의

- 통계값
평균 : μ
분산 : 𝜎2
표준편차 : 𝜎
- 표현
확률변수 X가 정규확률분포를 따른다 : X~N(μ,𝜎2)
- 분포의 모양
=> 모양은 평균과 분산에 의하여 결정
1) 평균

2) 분산

- 정규 확률변수의 합
가정 : 확률변수 X와 Y가 서로 독립이고, 모두 정규확률분포를 따른다.

- 정규분포의 누적확률 (Cumulative Distribution Function, CDF)
정규분포의 누적확률 𝐶𝐷𝐹(𝑥)는 구간 (−∞,𝑥] 에서 𝑓(𝑥) 아래의 면적과 같음.
즉, 𝐶𝐷𝐹(𝑥)=𝑃(−∞<𝑋≤𝑥)

4. 연속확률분포 : 표준정규확률분포
- 표준정규분포함수
정규분포함수는 구간 (−∞,+∞)에 대해서 정의

- 통계값
평균 : 0
분산 : 1
표준편차 : 1
- 표현
확률변수 X가 표준정규확률분포를 따른다 : X~N(0,1)
- 표준화
1) 표준화 목적
정규확률변수 X가 구간 a에서 b 사이에 속할 확률을 구하기 위해서
a와 b 사이의 정규곡선 아래 면적을 구해야 함.
모든 곡선들에 대한 별도의 표를 만들 수 없기 때문에, 모든 정규분포들에 대하여
같은 표를 사용할 수 있도록 표준화 과정 사용
2) 표준화 방법
확률변수 X가 정규분포를 따르는 경우 𝑋~𝑁(𝜇,𝜎2),
아래의 방식으로 X를 표준정규 확률변수로 변환.
그러면 𝑍~𝑁(0,1)
이것을 “표준화”라고 함.
즉 X -> Z로 변환

반대로 표준정규 확률변수 Z를 정규분포 𝑁(𝜇,𝜎2)를 따르는 확률변수로 변환도 가능.

- 표준정규분포 특징
x=𝜇 일 때, z=0
z=0에 대하여 대칭
곡선의 왼쪾에 있는 z값 음수
곡선의 오른쪽에 있는 z값 양수
분포의 총 면적은 1

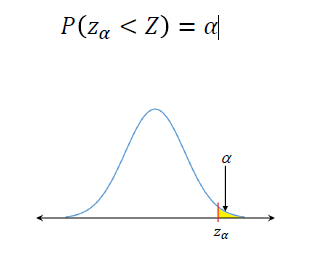
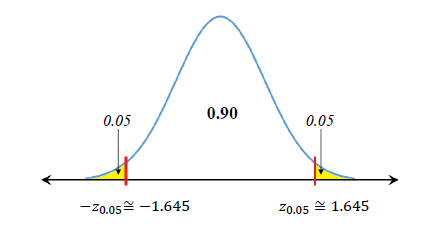
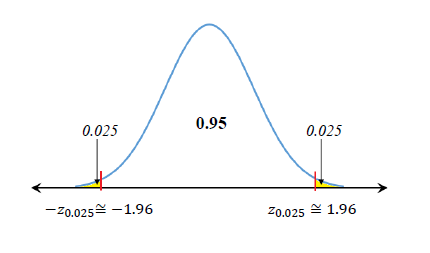
- 표준정규분포의 분위수 (Quantile of Standard Normal)
분위수 또는 백분위수는 신뢰구간 계산에 필요.
Za라고 표기하고 우측 꼬리의 면적이 α와 같은 변수값을 의미.
- 예시 문제


5. 연속확률분포 : 지수 확률분포(Exponential)
- 지수 확률분포함수
푸아송 사건 사이의 거리(시간)을 확률로 모델링하는 함수.

x는 양수(x>=0)
λ는 유일한 파라미터이고 양의 수치여야 함.
보통 1/λ는 시간의 의미.
- 표현
확률변수 X가 지수확률분포를 따른다 : X~Exp(λ)
- 통계값

- λ의 역할

- 지수분포의 누적확률 (Cumulative Distribution Function, CDF)
CDF(x)는 x가 증가하면 1로 수렴.

- 예시 문제

6. 연속확률분포 : 카이제곱분포(Chi Square)
- 카이제곱분포 개요
k개의 표준정규분포를 따르는 독립적인 확률변수 Xi~N(0,1)가 있을 떄,
카이제곱 확률변수 Q는 이들의 제곱의 합
k는 '자유도'라고 함

- 표현
확률변수 Q가 카이제곱 확률분포를 따른다 : Q~X2(k)
- 카이제곱 확률분포함수
카이제곱 확률분포함수는 구간 (0,+∞)에 대해서 정의

- 통계값

- 자유도 k의 역할

- 카이제곱 확률변수의 합
가정 : 확률변수 𝑄1와 𝑄2가 서로 독립이고, 카이제곱 확률분포를 따른다.


7. 연속확률분포 : 스튜던트 t 확률분포 (Student t)
- 스튜던트 t 확률분포 개요
Q ~ 𝜒2(v)이고 𝑍 ~ 𝑁(0,1)일때,
v는 카이제곱 확률변수의 '자유도'
자유도 v가 커질수록 스튜던트 t는 표준정규분포로 수렴.

- 표현
확률변수 T가 스튜던트 t 확률분포를 따른다 : T~t(v)
- 스튜던트 t 확률분포함수
스튜던트 t 확률분포함수는 구간 (−∞,+∞)에 대해서 정의

- 통계값
v>2일 경우에만

- 스튜던트 t 확률분포 특징
1) 스튜던트 t 분포함수는 통계에서 신뢰구간을 계산하는데 매우 중요한 역할을 함.
2) 표본에서 추출한 분산이 모분산과 크게 다를때 (표본의 크기가 작을 때),
표준정규분포의 분위수 대신에 스튜던트 t 분포의 분위수를 사용해서 신뢰구간의 하한과 상한을 계산한다.
3) 표본의 크기가 n일때 자유도는 𝜈=𝑛−1이다.
4) 표본의 크기가 커진다는 것은 자유도가 증가한다는 것과 같은 의미이고,
이때 스튜던트 t는 표준정규분포에 수렴하게 되니 표준정규분포의 분위수나 스튜던트 t의 분위수 큰 차이가 없게 된다.
- 자유도 v의 역할

8. 연속확률분포 : F 확률분포
- F 확률분포 개요
𝑄1 ~ 𝜒2(𝑑1)이고 𝑄2 ~ 𝜒2(𝑑2)일때,
𝑑1와 𝑑2는 카이제곱 확률변수의 '자유도'

- 표현
확률변수 X가 F 확률분포를 따른다 : 𝑋~ 𝐹(𝑑1,𝑑2)
- F 확률분포 특징
1) F 검정, 분산분석 (ANOVA) 등 활용.
2) 자유도 𝑑2가 커질수록 F분포는 카이제곱 𝑄1/𝑑1 로 수렴
- 통계값
평균 d2>2일 경우
분산 d2>4일 경우
최빈값 d1>2일 경우

- 자유도 d1,d2의 역할

'데이터과학 > 개념 : Statistics' 카테고리의 다른 글
| [통계기초] 통계분석 : 통계적 추정 : 점추정, 구간추정 (0) | 2020.04.18 |
|---|---|
| [통계기초] 통계분석 : 통계적 추정 : 기술통계, 기본개념 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 결합확률 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 이산확률 (0) | 2020.04.16 |
| [통계기초] 확률 : 기본개념 (0) | 2020.04.16 |




