| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Hadoop
- CNN
- 데이터시각화
- r
- pandas
- Deeplearning
- R프로그래밍
- R그래프
- AI
- 데이터처리
- 주가예측
- 데이터분석
- 데이터
- ggplot
- SQL
- 딥러닝
- NLP
- 자연어처리
- Python
- 그래프
- word2vec
- 빅데이터처리
- HIVE
- 하둡
- 빅데이터
- 그래프시각화
- 머신러닝
- R시각화
- 기계학습
- lstm
- Today
- Total
욱이의 냉철한 공부
[통계기초] 확률 : 기본개념 본문
* 자료출저 및 참고강의
패스트캠퍼스 올인원 패키지(금융공학/퀀트) 장순용 강사님 인터넷 강의
명지대 산업경영공학과 박윤선 교수님 통계학개론 강의
* 목차
확률 : 개본개념
1. 확률 기본용어
2. 수학적 확률 정의
3. 통계적 확률 정의
4. 확률의 기본 특성
5. 확률의 덧셈 : 여사건확률
6. 확률의 곱셈 : 조건부확률
1. 확률 기본용어
- 시행, 실험(experiment)
가능한 모든 결과를 알 수 있는 관찰 또는 실험.
같은 조건 아래에서 반복할 수 있음.
그 결과가 우연에 의해서 결정됨.
- 표본공간(sample space)
모든 단순사건들의 모임

- 단순사건, 근원사건(simple event)
실험으로부터 나오는 한 결과
확률이 적용되는 기본단위
실험이 시행 될 경우 오직 한 단순사건만 발생 할 수 있다.
각 단순사건에는 발생빈도를 측정하는 확률이 할당 될 수 있다.
e1, e2, e3,... eN
ex) 표본공간 : S = {1,2,3,4,5,6}
4의 눈이 나오는 사건 : E1 = {5} => 근원사건
홀수의 눈이 나오는 사건 : E2 = {1,3,5} => 사건, 부분집합
- 사건, 부분집합(event)
하나 이상의 단순사건들의 모임
표본공간의 부분집합.
- 전사건
S 전체
- 공사건
공집합. Φ
- 배반사건
두 사건이 동시에 일어날 수 없을 때

- 예시

2. 수학적 확률 정의
- 수학적 확률
1. 사건 A의 확률 P(A)는 "얼마나 자주" 사건 A가 발생하는지를 나타내는 척도.
2. N이 한 시행에 따라서 일어날 수 있는 모든 경우의 수이고, N(A)는 사건 A가 일어나는 경우의 수 일 때
수학적 확률 P(A)는 다음처럼 표기

- 예시 문제

3. 통계적 확률 정의
- 통계적(경험적) 확률
어떤 조건 아래에서 실험 또는 관측한 자료의 총수를 N이라 하고, 그 중에서 어떤 사건 A가 일어난 횟수를 N(A)라 할 때 상대도수는 다음과 같음

통계적확률 P(A)는 상대도수의 극한.

- 예시 문제

4. 확률의 기본 특성
- 확률의 기본 특성
1. 0 <= P(A) <= 1
2. P(S) = 1
3. P(Φ) = 0
4. P1 + P2 ..... +PN = 1 (근원사건 ei의 확률 pi를 모두 더하면 1)
5. 확률의 덧셈 : 여사건확률
- 확률의 덧셈
1) 사건 A, B

2) 사건 A, B 배반사건 (AΠB=Φ)
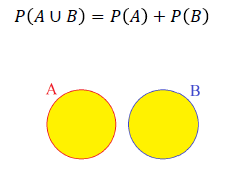
3) 사건 A, B, C 배반사건 (AΠB=Φ, AΠC=Φ, BΠC=Φ)

- 예시 문제


- 여사건의 확률
사건 A의 여(complement)사건은 A가 일어나지 않는 사건이며, Ac로 나타낸다.

- 예시 문제

6. 확률의 곱셈 : 조건부 확률
- 조건부 확률
확률이 0이 아닌 사건 A와 B에 대해서 사건 A가 일어났다는 전제로 사건 B가 일어날 확률

=> 관계 성립

- 종속사건
1) 사건 A와 B가 종속사건

2) 종속사건의 덧셈

- 독립사건
사건 A와 B가 종속사건

- 배반사건
사건 A와 B가 배반사건
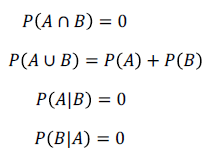
* 독립사건과 배반사건은 서로 무관한 다른 개념
- 예시 문제


7. 베이즈 정리
- 베이즈 정리( 베이즈 통계법)
조건부 확률에서 "베이즈 정리" 도출

=> 변형

- 예시 문제


'데이터과학 > 개념 : Statistics' 카테고리의 다른 글
| [통계기초] 통계분석 : 통계적 추정 : 점추정, 구간추정 (0) | 2020.04.18 |
|---|---|
| [통계기초] 통계분석 : 통계적 추정 : 기술통계, 기본개념 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 결합확률 (0) | 2020.04.18 |
| [통계기초] 확률변수와 확률분포함수 : 연속확률 (0) | 2020.04.17 |
| [통계기초] 확률변수와 확률분포함수 : 이산확률 (0) | 2020.04.16 |




